
科目: 来源: 题型:
【题目】如图,我海监船在![]() 岛海域例行维权巡航,某时刻航行至
岛海域例行维权巡航,某时刻航行至![]() 处,此时测得其东北方向与它相距
处,此时测得其东北方向与它相距![]() 海里的
海里的![]() 处有一外国船只,且
处有一外国船只,且![]() 岛位于海监船正东
岛位于海监船正东![]() 海里处.
海里处.
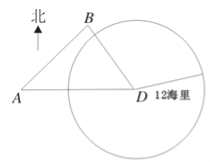
(1)求此时该外国船只与![]() 岛的距离;
岛的距离;
(2)观测中发现,此外国船只正以每小时![]() 海里的速度沿正南方向航行,为了将该船拦截在离
海里的速度沿正南方向航行,为了将该船拦截在离![]() 岛
岛![]() 海里处,不让其进入
海里处,不让其进入![]() 岛
岛![]() 海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据:
海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】定义在 ![]() 上的函数
上的函数 ![]() 若同时满足:①存在
若同时满足:①存在 ![]() ,使得对任意的
,使得对任意的 ![]() ,都有
,都有 ![]() ;②
;② ![]() 的图象存在对称中心.则称
的图象存在对称中心.则称 ![]() 为“
为“![]() 函数”.已知函数
函数”.已知函数 ![]() 和
和 ![]() ,则以下结论一定正确的是
,则以下结论一定正确的是 ![]()
A. ![]() 和
和 ![]() 都是
都是 ![]() 函数 B.
函数 B. ![]() 是
是 ![]() 函数,
函数, ![]() 不是
不是 ![]() 函数
函数
C. ![]() 不是
不是 ![]() 函数,
函数, ![]() 是
是 ![]() 函数 D.
函数 D. ![]() 和
和 ![]() 都不是
都不是 ![]() 函数
函数
查看答案和解析>>
科目: 来源: 题型:
【题目】从5名男生和4名女生中选出4人去参加座谈会,问:
(1)如果4人中男生和女生各选2人,有多少种选法?
(2)如果男生中的甲与女生中的乙至少要有1人在内,有多少种选法?
(3)如果4人中必须既有男生又有女生,有多少种选法?
查看答案和解析>>
科目: 来源: 题型:
【题目】在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6名选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图,为了增加结果的神秘感,主持人故意没有给出甲、乙两班最后一位选手的成绩,只是告知大家,如果某位选手的成绩高于90分(不含90分),则直接“晋级”.
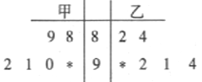
(1)求乙班总分超过甲班的概率;
(2)主持人最后宣布:甲班第六位选手的得分是90分,乙班第六位选手的得分是97分,
①请你从平均分和方差的角度来分析两个班的选手的情况;
②主持人从甲乙两班所有选手成绩中分别随机抽取2个,记抽取到“晋级”选手的总人数为![]() ,求
,求![]() 的分
的分
布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为线段
分别为线段![]() 、
、![]() 的中点,
的中点,![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 上一点,且
上一点,且![]() ,
,![]() .
.
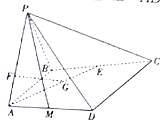
(1)确定点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ;
;
(2)试问:直线![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的大小为
所成锐二面角的大小为![]() ,若存在,求
,若存在,求![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙同学参加学校“一站到底”闯关活动,活动规则:①依次闯关过程中,若闯关成功则继续答题;若没通关则被淘汰;②每人最多闯3关;③闯第一关得10分,闯第二关得20分,闯第三关得30分,一关都没过则没有得分.已知甲每次闯关成功的概率为![]() ,乙每次闯关成功的概率为
,乙每次闯关成功的概率为![]() .
.
(Ⅰ)设乙的得分总数为![]() ,求
,求![]() 得分布列和数学期望;
得分布列和数学期望;
(Ⅱ)求甲恰好比乙多30分的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() 为线段
为线段![]() 上的一动点.
上的一动点.
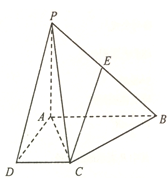
(Ⅰ)若![]() 为线段
为线段![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)当直线![]() 与平面
与平面![]() 所成角小于
所成角小于![]() ,求
,求![]() 长度的取值范围.
长度的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com