
科目: 来源: 题型:
【题目】某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如下柱状图:

(1)从样本中任意选取2名学生,求恰好有一名学生的打分不低于4分的概率;
(2)若以这100人打分的频率作为概率,在该校随机选取2名学生进行打分(学生打分之间相互独立)记![]() 表示两人打分之和,求
表示两人打分之和,求![]() 的分布列和
的分布列和![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为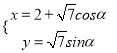 (其中
(其中![]() 为参数),曲线
为参数),曲线![]() :
: ![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() (
(![]() )与曲线
)与曲线![]() ,
, ![]() 分别交于
分别交于![]() ,
, ![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择;
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率为![]() .第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
.第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为![]() ,每次中奖均可获奖金400元.
,每次中奖均可获奖金400元.
(1)求某员工选择方案甲进行抽奖所获奖金![]() (元)的分布列;
(元)的分布列;
(2)某员工选择方案乙与选择方案甲进行抽奖,试比较哪个方案更划算?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知中心在原点![]() ,焦点在
,焦点在![]() 轴上的椭圆,离心率
轴上的椭圆,离心率![]() ,且椭圆过点
,且椭圆过点![]() .
.
(1)求椭圆的方程;
(2)设椭圆左、右焦点分别为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,则
,则![]() 的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】五一期间,某商场决定从![]() 种服装、
种服装、![]() 种家电、
种家电、![]() 种日用品中,选出
种日用品中,选出![]() 种商品进行促销活动.
种商品进行促销活动.
(1)试求选出![]() 种商品中至少有一种是家电的概率;
种商品中至少有一种是家电的概率;
(2)商场对选出的某商品采用抽奖方式进行促销,即在该商品现价的基础上将价格提高![]() 元,规定购买该商品的顾客有
元,规定购买该商品的顾客有![]() 次抽奖的机会: 若中一次奖,则获得数额为
次抽奖的机会: 若中一次奖,则获得数额为![]() 元的奖金;若中两次奖,则获得数额为
元的奖金;若中两次奖,则获得数额为![]() 元的奖金;若中三次奖,则共获得数额为
元的奖金;若中三次奖,则共获得数额为 ![]() 元的奖金. 假设顾客每次抽奖中奖的概率都是
元的奖金. 假设顾客每次抽奖中奖的概率都是![]() ,请问: 商场将奖金数额
,请问: 商场将奖金数额![]() 最高定为多少元,才能使促销方案对商场有利?
最高定为多少元,才能使促销方案对商场有利?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)设![]() ,
, ![]() 是曲线
是曲线![]() 图象上的两个相异的点,若直线
图象上的两个相异的点,若直线![]() 的斜率
的斜率![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() 有两个极值点
有两个极值点![]() ,
, ![]() ,且
,且![]() ,若
,若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com