
科目: 来源: 题型:
【题目】设椭圆![]() 的焦点在
的焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,抛物线
,抛物线![]() 的焦点在
的焦点在![]() 轴上,
轴上, ![]() 的中心和
的中心和![]() 的顶点均为原点,点
的顶点均为原点,点 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,
(1)求曲线![]() ,
, ![]() 的标准方程;
的标准方程;
(2)请问是否存在过抛物线![]() 的焦点
的焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() ,使得以线段
,使得以线段![]() 为直径的圆过原点
为直径的圆过原点![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 的通项公式是
的通项公式是![]() .
.
(1)判断![]() 是否是数列
是否是数列![]() 中的项;
中的项;
(2)试判断数列![]() 中的各项是否都在区间
中的各项是否都在区间![]() 内;
内;
(3)试判断在区间![]() 内是否有无穷数列
内是否有无穷数列![]() 中的项?若有,是第几项?若没有,请说明理由.
中的项?若有,是第几项?若没有,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】天气预报是气象专家根据预测的气象资料和专家们的实际经验,经过分析推断得到的,在现实的生产生活中有着重要的意义,某快餐企业的营销部门对数据分析发现,企业经营情况与降雨填上和降雨量的大小有关.
(1)天气预报所,在今后的三天中,每一天降雨的概率为40%,该营销部分通过设计模拟实验的方法研究三天中恰有两天降雨的概率,利用计算机产生0大9之间取整数值的随机数,并用![]() 表示下雨,其余
表示下雨,其余![]() 个数字表示不下雨,产生了20组随机数:
个数字表示不下雨,产生了20组随机数:
![]()
求由随机模拟的方法得到的概率值;
(2)经过数据分析,一天内降雨量的大小![]() (单位:毫米)与其出售的快餐份数
(单位:毫米)与其出售的快餐份数![]() 成线性相关关系,该营销部门统计了降雨量与出售的快餐份数的数据如下:
成线性相关关系,该营销部门统计了降雨量与出售的快餐份数的数据如下:
![]()
试建立![]() 关于
关于![]() 的回归方程,为尽量满足顾客要求又不在造成过多浪费,预测降雨量为6毫米时需要准备的快餐份数.(结果四舍五入保留整数)
的回归方程,为尽量满足顾客要求又不在造成过多浪费,预测降雨量为6毫米时需要准备的快餐份数.(结果四舍五入保留整数)
附注:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
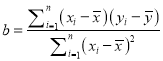 ,
, ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=f(x)满足f(﹣2)=f(4)=﹣16,且f(x)最大值为2.
(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)在[t,t+1](t>0)上的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点
,以极点![]() 为坐标原点,极轴为
为坐标原点,极轴为![]() 的正半轴建立平面直角坐标系
的正半轴建立平面直角坐标系![]() .
.
(1)求![]() 和
和![]() 的参数方程;
的参数方程;
(2)已知射线![]() ,将
,将![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,且
,且![]() 与
与![]() 交于
交于![]() 两点,
两点, ![]() 与
与![]() 交于
交于![]() 两点,求
两点,求![]() 取得最大值时点
取得最大值时点![]() 的极坐标.
的极坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合 计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合 计 | 70 | 30 | 100 |
⑴根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差
异”;
⑵已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机
抽取3人,求至多有1人喜欢甜品的概率.
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
附: 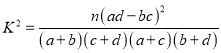 ,
,
查看答案和解析>>
科目: 来源: 题型:
【题目】为丰富人民群众业余生活,某市拟建设一座江滨公园,通过专家评审筛选处建设方案A和B向社会公开征集意见,有关部分用简单随机抽样方法调查了500名市民对这两种方案的看法,结果用条形图表示如下:
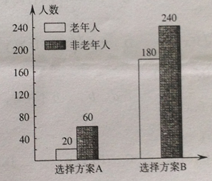
(1)根据已知条件完成下面![]() 列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过
列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过![]() 的前提下认为是否选择方案A和年龄段有关?
的前提下认为是否选择方案A和年龄段有关?
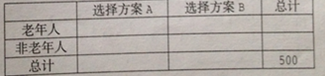
(2)根据(1)的结论,能否提出一个更高的调查方法,使得调查结果更具代表性,说明理由.
附:

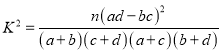
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com