
科目: 来源: 题型:
【题目】设全集U={(x,y)|x,y∈R},集合M={(x,y)| ![]() =1},N={(x,y)|y=x+1},则N∩(UM)等于( )
=1},N={(x,y)|y=x+1},则N∩(UM)等于( )
A.
B.{(2,3)}
C.(2,3)
D.{(x,y)|y=x+1}
查看答案和解析>>
科目: 来源: 题型:
【题目】若二次函数f(x)=x2+bx+c满足f(2)=f(﹣2),且函数的f(x)的一个零点为1. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)对任意的 ![]() ,4m2f(x)+f(x﹣1)≥4﹣4m2恒成立,求实数m的取值范围.
,4m2f(x)+f(x﹣1)≥4﹣4m2恒成立,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择;
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率为![]() .第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
.第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为![]() ,每次中奖均可获奖金400元.
,每次中奖均可获奖金400元.
(1)求某员工选择方案甲进行抽奖所获奖金![]() (元)的分布列;
(元)的分布列;
(2)某员工选择方案乙与选择方案甲进行抽奖,试比较哪个方案更划算?
查看答案和解析>>
科目: 来源: 题型:
【题目】在某单位的职工食堂中,食堂每天以![]() 元/个的价格从面包店购进面包,然后以
元/个的价格从面包店购进面包,然后以![]() 元/个的价格出售.如果当天卖不完,剩下的面包以
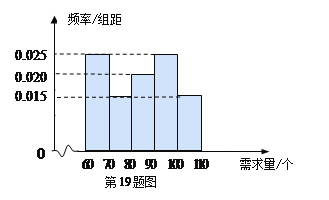
元/个的价格出售.如果当天卖不完,剩下的面包以![]() 元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了
元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了![]() 个面包,以
个面包,以![]() (单位:个,
(单位:个, ![]() )表示面包的需求量,
)表示面包的需求量, ![]() (单位:元)表示利润.
(单位:元)表示利润.
(Ⅰ)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅱ)求食堂每天面包需求量的中位数;
(Ⅲ)根据直方图估计利润![]() 不少于
不少于![]() 元的概率;
元的概率;
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=log2(4x)log2(2x)的定义域为 ![]() . (Ⅰ)若t=log2x,求t的取值范围;
. (Ⅰ)若t=log2x,求t的取值范围;
(Ⅱ)求y=f(x)的最大值与最小值,并求取得最值时对应的x的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=x+ ![]() ,且函数y=f(x)的图像经过点(1,2).
,且函数y=f(x)的图像经过点(1,2).
(1)求m的值;
(2)判断函数的奇偶性并加以证明;
(3)证明:函数f(x)在(1,+∞)上是增函数.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,过椭圆
中,过椭圆![]() 右焦点的直线
右焦点的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点, ![]() 为
为![]() 的中点,且直线
的中点,且直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设另一直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,原点
两点,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x2﹣2x. 
(1)画出偶函数f(x)的图像的草图,并求函数f(x)的单调递增区间;
(2)当直线y=k(k∈R)与函数y=f(x)恰有4个交点时,求k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=x|x﹣a|
(1)若函数y=f(x)+x在R上是增函数,求实数a的取值范围;
(2)若对任意x∈[1,2]时,函数f(x)的图像恒在y=1图像的下方,求实数a的取值范围;
(3)设a≥2时,求f(x)在区间[2,4]内的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com