
科目: 来源: 题型:
【题目】![]() 是等边三角形,边长为4,
是等边三角形,边长为4, ![]() 边的中点为
边的中点为![]() ,椭圆
,椭圆![]() 以
以![]() ,
, ![]() 为左、右两焦点,且经过
为左、右两焦点,且经过![]() 、
、![]() 两点。
两点。
(1)求该椭圆的标准方程;
(2)过点![]() 且
且![]() 轴不垂直的直线
轴不垂直的直线![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点,求证:直线
两点,求证:直线![]() 与
与![]() 的交点在一条定直线上.
的交点在一条定直线上.
查看答案和解析>>
科目: 来源: 题型:
【题目】经销商经销某种农产品,在一个销售季度内,每售出![]() 该产品获利润500元,未售出的产品,每
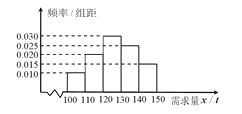
该产品获利润500元,未售出的产品,每![]() 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了![]() 该农产品.以
该农产品.以![]() (
(![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, ![]() (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
(Ⅰ)将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)根据直方图估计利润![]() 不少于57000元的概率.
不少于57000元的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=x2﹣2x|x﹣a|(其中a∈R).
(1)当a=1时,求函数f(x)的值域;
(2)若y=f(x)在[0,2]上的最小值为﹣1,求a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知某运动员每次投篮命中的概率等于![]() .现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为__________.
查看答案和解析>>
科目: 来源: 题型:
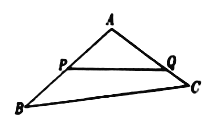
【题目】如图,某生态园将一块三角形地![]() 的一角
的一角![]() 开辟为水果园,已知角
开辟为水果园,已知角![]() 为
为![]() ,
, ![]() 的长度均大于200米,现在边界
的长度均大于200米,现在边界![]() 处建围墙,在
处建围墙,在![]() 处围竹篱笆.
处围竹篱笆.
(1)若围墙![]() 、
、![]() 总长度为200米,如何可使得三角形地块
总长度为200米,如何可使得三角形地块![]() 面积最大?
面积最大?
(2)已知竹篱笆长为![]() 米,
米, ![]() 段围墙高1米,
段围墙高1米, ![]() 段围墙高2米,造价均为每平方米100元,若
段围墙高2米,造价均为每平方米100元,若![]() ,求围墙总造价的取值范围.
,求围墙总造价的取值范围.
查看答案和解析>>
科目: 来源: 题型:
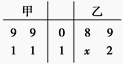
【题目】如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题(满分12分)的得分情况.乙组某个数据的个位数模糊,记为x,已知甲、乙两组的平均成绩相同.
(1)求x的值,并判断哪组学生成绩更稳定;
(2)在甲、乙两组中各抽出一名同学,求这两名同学的得分之和低于20分的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 |
|
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) |
| 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55] | 15 | 0.3 |
(1)补全频率分布直方图并求![]() 的值;
的值;
(2)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.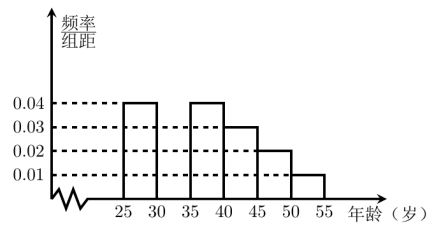
查看答案和解析>>
科目: 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com