【题目】在测试中，客观题难度的计算公式为，其中为第题的难度， 为答对该题的人数， 为参加测试的总人数．现对某校高三年级240名学生进行一次测试，共5道客观题，测试前根据对学生的了解，预估了每道题的难度，如表所示：

测试后，从中随机抽取了20名学生的答题数据进行统计，结果如表：

（Ⅰ）根据题中数据，估计中240名学生中第5题的实测答对人数；

（Ⅱ）从抽样的20名学生中随机抽取2名学生，记这2名学生中第5题答对的人数为，求的分布列和数学期望；

（Ⅲ）试题的预估难度和实测难度之间会有偏差．设为第题的实测难度，请用和设计一个统计量，并制定一个标准来判断本次测试对难度的预估是否合理．

【题目】如图，已知椭圆： 的离心率为， 为椭圆的右焦点， ， .

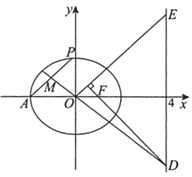
（Ⅰ）求椭圆的方程；

（Ⅱ）设为原点， 为椭圆上一点， 的中点为，直线与直线交于点，过且平行于的直线与直线交于点．求证： ．

【题目】如图，在正四棱锥中， ， ， 分别为， 的中点．

（Ⅰ）求证： 平面；

（Ⅱ）求异面直线与所成角的余弦值；

（Ⅲ）若平面与棱交于点，求的值．

【题目】现有道数学题，其中道选择题， 道填空题，小明从中任取道题，求：

（1）所取的道题都是选择题的概率；

（2）所取的道题不是同一种题型的概率.

【题目】设数列{an}的前n项和为Sn ， 令Tn= ，称Tn为数列a1 ， a2 ， …，an的“理想数”，已知数列a1 ， a2 ， …，a502的“理想数”为2012，那么数列2，a1 ， a2 ， …，a502的“理想数”为（ ）
A.2010
B.2011
C.2012
D.2013

【题目】设O为坐标原点，点P的坐标（x﹣2，x﹣y）
（1）在一个盒子中，放有标号为1，2，3的三张卡片，现从此盒中有放回地先后抽到两张卡片的标号分别记为x，y，求|OP|的最大值，并求事件“|OP|取到最大值”的概率；
（2）若利用计算机随机在[0，3]上先后取两个数分别记为x，y，求P点在第一象限的概率．

【题目】某出租车公司响应国家节能减排的号召，已陆续购买了140辆纯电动汽车作为运营车辆，目前我国主流纯电动汽车按续航里程数．（单位：公里）分为3类，即类：，类：， 类：，该公司对这140辆车的行驶总里程进行统计，结果如下表：

（1）从这140辆汽车中任取一辆，求该车行驶总里程超过10万公里的概率；

（2）公司为了了解这些车的工作状况，决定抽取了14辆车进行车况分析，按表中描述的六种情况进行分层抽样，设从类车中抽取了辆车．

①求的值；

②如果从这辆车中随机选取两辆车，求恰有一辆车行驶总里程超过10万公里的概率．

（1）若某位顾客消费128元，求返券金额不低于30元的概率；

（2）若某位顾客恰好消费280元，并按规则参与了活动，他获得返券的金额记为（元）．求随机变量的分布列和数学期望．

【题目】已知数列为公差不为的等差数列， 为前项和， 和的等差中项为，且．令数列的前项和为．

（1）求及；

（2）是否存在正整数成等比数列？若存在，求出所有的的值；若不存在，请说明理由．

【题目】如图所示，在四棱锥中， 平面是的中点， 是上的点且为边上的高.

（1）证明： 平面；

（2）若，求三棱锥的体积；

（3）在线段上是否存在这样一点，使得平面?若存在，说出点的位置.