
科目: 来源: 题型:
【题目】某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( ) 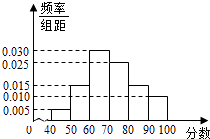
A.588
B.480
C.450
D.120
查看答案和解析>>
科目: 来源: 题型:
【题目】某班级有50名学生,其中有30名男生和20名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86,94,88,92,90,五名女生的成绩分别为88,93,93,88,93,下列说法正确的是( )
A.这种抽样方法是一种分层抽样
B.这种抽样方法是一种系统抽样
C.这五名男生成绩的方差大于这五名女生成绩的方差
D.该班男生成绩的平均数大于该班女生成绩的平均数
查看答案和解析>>
科目: 来源: 题型:
【题目】潍坊文化艺术中心的观光塔是潍坊市的标志性建筑,某班同学准备测量观光塔![]() 的高度
的高度![]() (单位:米),如图所示,垂直放置的标杆
(单位:米),如图所示,垂直放置的标杆![]() 的高度
的高度![]() 米,已知
米,已知![]() ,
, ![]() .
.
(1)该班同学测得![]() 一组数据:
一组数据: ![]() ,请据此算出
,请据此算出![]() 的值;
的值;
(2)该班同学分析若干测得的数据后,发现适当调整标杆到观光塔的距离![]() (单位:米),使
(单位:米),使![]() 与
与![]() 的差较大,可以提高测量精确度,若观光塔高度为136米,问
的差较大,可以提高测量精确度,若观光塔高度为136米,问![]() 为多大时,
为多大时, ![]() 的值最大?
的值最大?

查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=2sin2( ![]() +x)+
+x)+ ![]() (sin2x﹣cos2x),x∈[
(sin2x﹣cos2x),x∈[ ![]() ,
, ![]() ].
].
(1)求 ![]() 的值;
的值;
(2)求f(x)的单调区间;
(3)若不等式|f(x)﹣m|<2恒成立,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,
中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2, ![]() .
.
(1)求证:PD⊥平面PAB;
(2)求直线PB与平面PCD所成角的正弦值.
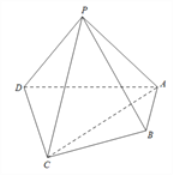
查看答案和解析>>
科目: 来源: 题型:
【题目】据统计,某物流公司每天的业务中,从甲地到乙地的可配送的货物量![]() 的频率分布直方图,如图所示,将频率视为概率,回答以下问题.
的频率分布直方图,如图所示,将频率视为概率,回答以下问题.
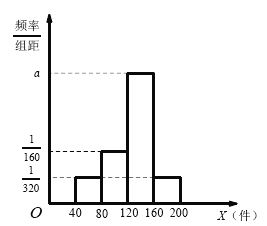
(1)求该物流公司每天从甲地到乙地平均可配送的货物量;
(2)该物流公司拟购置货车专门运营从甲地到乙地的货物,一辆货车每天只能运营一趟,每辆车每
趟最多只能装载40 件货物,满载发车,否则不发车。若发车,则每辆车每趟可获利1000 元;若未发车,
则每辆车每天平均亏损200 元。为使该物流公司此项业务的营业利润最大,该物流公司应该购置几辆货
车?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的长轴长为6,且椭圆
的长轴长为6,且椭圆![]() 与圆
与圆![]() :
: ![]() 的公共弦长为
的公共弦长为![]() .
.
(1)求椭圆![]() 的方程.
的方程.
(2)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,
, ![]() ,试判断在
,试判断在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为以
为以![]() 为底边的等腰三角形.若存在,求出点
为底边的等腰三角形.若存在,求出点![]() 的横坐标的取值范围,若不存在,请说明理由.
的横坐标的取值范围,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com