
科目: 来源: 题型:
【题目】已知定义在(﹣∞,0)∪(0,+∞)上的奇函数f(x)满足f(2)=0,且在(﹣∞,0)上是增函数;又定义行列式![]() =a1a4﹣a2a3; 函数g(θ)=
=a1a4﹣a2a3; 函数g(θ)=![]() (其中0≤θ≤
(其中0≤θ≤![]() ).
).
(1)证明:函数f(x)在(0,+∞)上也是增函数;
(2)若函数g(θ)的最大值为4,求m的值;
(3)若记集合M={m|任意的0≤θ≤![]() , g(θ)>0},N={m|任意的0≤θ≤
, g(θ)>0},N={m|任意的0≤θ≤![]() , f[g(θ)]<0},求M∩N.
, f[g(θ)]<0},求M∩N.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米,某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-![]() 表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)当k=2时,求炮的射程;
(2)求炮的最大射程;
(3)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以其中它?请说明理由.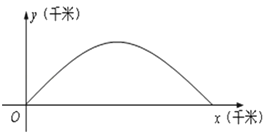
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
, ![]() ,
, ![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 过点
过点![]() ,且
,且![]() 和以
和以![]() 为圆
为圆![]() 相切.
相切.
(1)求圆![]() 的方程;
的方程;
(2)在圆![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在,求出所有的点
,若存在,求出所有的点![]() 的坐标;若不存在说明理由;
的坐标;若不存在说明理由;
(3)若不过![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点,且满足
两点,且满足![]() ,
, ![]() ,
, ![]() 的斜率依次为等比数列,求直线
的斜率依次为等比数列,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知a<1,集合A={x|x<a﹣2或x>﹣a},集合B={x|cos(xπ)=1},全集U=R.
(1)当a=0时,求(UA)∩B;
(2)若(UA)∩B恰有2个元素,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市为了引导居民合理用水,居民生活用水实行二级阶梯式水价计量办法,具体如下:第一阶梯,每户居民月用水量不超过12吨,价格为4元/吨;第二阶梯,每户居民月用水量超过12吨,超过部分的价格为8元/吨.为了了解全市居民月用水量的分布情况,通过抽样获得了100户居民的月用水量(单位:吨),将数据按照![]() ,
, ![]() ,…,
,…, ![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.
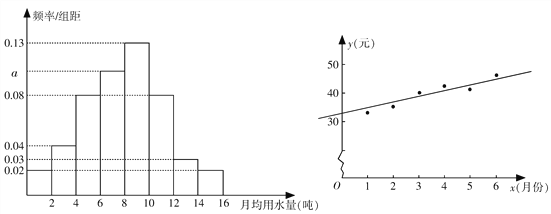
(图1) (图2)
(Ⅰ)求频率分布直方图中字母![]() 的值,并求该组的频率;
的值,并求该组的频率;
(Ⅱ)通过频率分布直方图,估计该市居民每月的用水量的中位数![]() 的值(保留两位小数);
的值(保留两位小数);
(Ⅲ)如图2是该市居民张某2016年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() . 若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
. 若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=4x﹣2x+1+3,当x∈[﹣2,1]时,f(x)的最大值为m,最小值为n,
(1)若角α的终边经过点P(m,n),求sinα+cosα的值;
(2)g(x)=mcos(nx+![]() )+n,求g(x)的最大值及自变量x的取值集合.
)+n,求g(x)的最大值及自变量x的取值集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com