【题目】已知函数．

（Ⅰ）讨论函数的单调性；

（Ⅱ）证明： 时， ；

（Ⅲ）比较三个数： ， ， 的大小（为自然对数的底数），请说明理由．

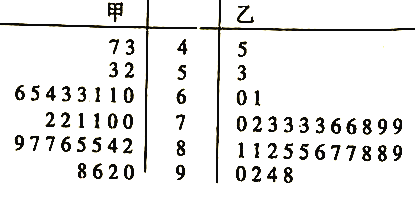
（Ⅰ）若乙校每位学生被抽取的概率为0.15，求乙校参赛学生总人数；

（Ⅱ）根据茎叶图，从平均水平与波动情况两个方面分析甲、乙两校参赛学生成绩（不要求计算）；

（Ⅲ）从样本成绩低于60分的学生中随机抽取3人，求3人不在同一学校的概率．

【题目】已知二次函数f（x）=x2+2bx+c（b，c∈R）．
（1）若函数y=f（x）的零点为﹣1和1，求实数b，c的值；
（2）若f（x）满足f（1）=0，且关于x的方程f（x）+x+b=0的两个实数根分别在区间（﹣3，﹣2），（0，1）内，求实数b的取值范围．

【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点．研究表明：“活水围网”养鱼时，某种鱼在一定的条件下，每尾鱼的平均生长速度v（单位：千克/年）是养殖密度x （单位：尾/立方米）的函数．当x不超过4尾/立方米时，v的值为2千克/年；当4＜x≤20时，v是x的一次函数，当x达到20尾/立方米时，因缺氧等原因，v的值为0千克/年．
（1）当0＜x≤20时，求v关于x的函数表达式；
（2）当养殖密度x为多大时，鱼的年生长量（单位：千克/立方米）可以达到最大？并求出最大值．

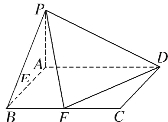
【题目】已知在四棱锥中，底面是矩形，且，，平面，、分别是线段、的中点．

（1）证明：

（2）在线段上是否存在点，使得∥平面，若存在，确定点的位置；若不存在，说明理由．

（3）若与平面所成的角为，求二面角的余弦值

【题目】已知椭圆： 的离心率为，顺次连接椭圆的四个顶点得到的四边形的面积为16．

（Ⅰ）求椭圆的方程；

（Ⅱ）过椭圆的顶点的直线交椭圆于另一点，交轴于点，若、、成等比数列，求直线的斜率．

【题目】（本题满分15分）如图，在四棱锥中，平面PAD⊥平面ABCD， ，，E是BD的中点．

（Ⅰ）求证：EC//平面APD；

（Ⅱ）求BP与平面ABCD所成角的正切值；

（Ⅲ）求二面角的正弦值．

【题目】已知全集U=R，集合A={x|4≤2x＜128}，B={x|1＜x≤6}，M={x|a﹣3＜x＜a+3}．
（1）求A∩UB；
（2）若M∪UB=R，求实数a的取值范围．

【题目】下列几个命题
①奇函数的图象一定通过原点
②函数y= 是偶函数，但不是奇函数
③函数f（x）=ax﹣1+3的图象一定过定点P，则P点的坐标是（1，4）
④若f（x+1）为偶函数，则有f（x+1）=f（﹣x﹣1）
⑤若函数f（x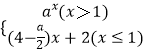）= 在R上的增函数，则实数a的取值范围为[4，8）
其中正确的命题序号为 ．