
科目: 来源: 题型:
【题目】已知函数f(x)=x2﹣2x+t,g(x)=x2﹣t(t∈R)
(1)当x∈[2,3]时,求函数f(x)的值域(用t表示)
(2)设集合A={y|y=f(x),x∈[2,3]},B={y|y=|g(x)|,x∈[2,3]},是否存在正整数t,使得A∩B=A.若存在,请求出所有可能的t的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知{an}是等比数列,{bn}是等差数列,且a1=b1=1,a1+a2=b4 , b1+b2=a2 .
(1)求{an}与{bn}的通项公式;
(2)记数列{an+bn}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目: 来源: 题型:
【题目】若钝角三角形的三边长和面积都是整数,则称这样的三角形为“钝角整数三角形”,下列选项中能构成一个“钝角整数三角形”三边长的是( )
A.2,3,4
B.2,4,5
C.5,5,6
D.4,13,15
查看答案和解析>>
科目: 来源: 题型:
【题目】已知⊙O:x2+y2=1和定点A(2,1),由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足|PQ|=|PA|.
(1)求实数a,b间满足的等量关系;
(2)求线段PQ长的最小值;
(3)若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图△ABC是等腰三角形,BA=BC,DC⊥平面ABC,AE∥DC,若AC=2且BE⊥AD,则( ) 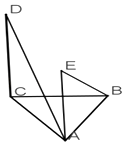
A.AB+BC有最大值
B.AB+BC有最小值
C.AE+DC有最大值
D.AE+DC有最小值
查看答案和解析>>
科目: 来源: 题型:
【题目】设α,β是两个不同的平面,m,n是两条不同的直线,有如下两个命题:q:若m⊥α,n⊥β且m∥n,则α∥β;q:若m∥α,n∥β且m∥n,则α∥β.( )
A.命题q,p都正确
B.命题p正确,命题q不正确
C.命题q,p都不正确
D.命题q不正确,命题p正确
查看答案和解析>>
科目: 来源: 题型:
【题目】四面体ABCD中,AB和CD为对棱.设AB=a,CD=b,且异面直线AB与CD间的距离为d,夹角为θ.
(Ⅰ)若θ= ![]() ,且棱AB垂直于平面BCD,求四面体ABCD的体积;
,且棱AB垂直于平面BCD,求四面体ABCD的体积;
(Ⅱ)当θ= ![]() 时,证明:四面体ABCD的体积为一定值;
时,证明:四面体ABCD的体积为一定值;
(Ⅲ)求四面体ABCD的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点. 
(1)求证:平面PAB∥平面EFG;
(2)证明:平面EFG⊥平面PAD;
(3)在线段PB上确定一点Q,使PC⊥平面ADQ,并给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com