
科目: 来源: 题型:
【题目】关于平面向量,有下列四个命题:
①若 ![]() .
.
② ![]() =(1,1),
=(1,1), ![]() =(2,x),若
=(2,x),若 ![]() 与
与 ![]() 平行,则x=2.
平行,则x=2.
③非零向量 ![]() 和
和 ![]() 满足|
满足| ![]() |=|
|=| ![]() |=|
|=| ![]() |,则
|,则 ![]() 与
与 ![]() 的夹角为60°.
的夹角为60°.
④点A(1,3),B(4,﹣1),与向量 ![]() 同方向的单位向量为(
同方向的单位向量为( ![]() ).
).
其中真命题的序号为 . (写出所有真命题的序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定义在R上的函数f(x)=Asin(ωx+φ)(x>0,A>0)的图象如图所示. 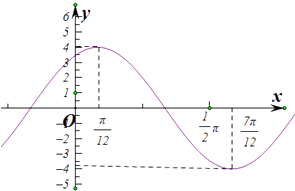
(1)求函数f(x)的解析式;
(2)写出函数f(x)的单调递增区间
(3)设不相等的实数,x1 , x2∈(0,π),且f(x1)=f(x2)=﹣2,求x1+x2的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,小区的两个出入口设置在点A及点C处,且小区里有一条平行于BO的小路CD,已知某人从C沿CD走到D用了10分钟,从D沿DA走到A用了6分钟,若此人步行的速度为每分钟50米,求该扇形的半径OA的长(精确到1米) 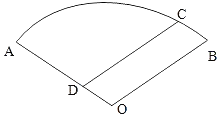
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4—4:坐标系与参数方程
点P是曲线C1:(x-2)2+y2=4上的动点,以坐标原点O为极点,x轴的正半轴为极轴
建立极坐标系,将点P绕极点O逆时针90得到点Q,设点Q的轨迹为曲线C2.
求曲线C1,C2的极坐标方程;
射线=![]() (>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积
(>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数F(x)= ![]() ,其中f(x)=log2(x2+1),g(x)=log2(|x|+7).
,其中f(x)=log2(x2+1),g(x)=log2(|x|+7).
(1)在实数集R上用分段函数形式写出函数F(x)的解析式;
(2)求函数F(x)的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某早餐店每天制作甲、乙两种口味的糕点共n(nN*)份,每份糕点的成本1元,售价2元,如果当天卖不完,剩下的糕点作废品处理.该早餐店发现这两种糕点每天都有剩余,为此整理了过往100天这两种糕点的日销量(单位:份),得到如下的统计数据:
甲口味糕点日销量 | 48 | 49 | 50 | 51 |
天数 | 20 | 40 | 20 | 20 |
乙口味糕点日销量 | 48 | 49 | 50 | 51 |
天数 | 40 | 30 | 20 | 10 |
以这100天记录的各销量的频率作为各销量的概率,假设这两种糕点的日销量相互独立.
(1)记该店这两种糕点每日的总销量为X份,求X的分布列
(2)早餐店为了减少浪费,提升利润,决定调整每天制作糕点的份数
①若产生浪费的概率不超过0.6,求n的最大值;
②以销售这两种糕点的日总利润的期望值为决策依据,在每天所制糕点能全部卖完与n=98之中选其一,应选哪个?
查看答案和解析>>
科目: 来源: 题型:
【题目】暑假期间小辉计划在8月11日至8月20日期间调研某商业中心周边停车场停车状况,根据停车场统计数据,该停车场在此期间“停车难易度”(即停车数量与核定的最大瞬时容量之比,40%以下为较易,40%~60%为一般,60%以上为较难),情况如图所示,小辉随机选择8月11日至8月19日中的某一天达到该商业中心,并连续调研2天.
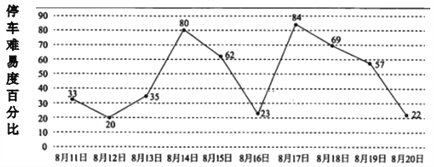
(Ⅰ)求小辉连续两天都遇上停车场较难的概率;
(Ⅱ)设![]() 是小辉调研期间遇上停车较易的天数,求
是小辉调研期间遇上停车较易的天数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)由图判断从哪天开始连续三天停车难易度的方差最大?(结论不要求证明)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知菱形ABCD的边长为2,∠BAD=120°,点E,F分别在边BC,DC上, ![]() =λ
=λ ![]() ,
, ![]() =μ
=μ ![]() ,若
,若 ![]()
![]() =1,
=1, ![]()
![]() =﹣
=﹣ ![]() ,则λ+μ=( )
,则λ+μ=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com