
科目: 来源: 题型:
【题目】如图,PA垂直于矩形ABCD所在的平面,AD=PA=2,CD=2 ![]() ,E、F分别是AB、PD的中点.
,E、F分别是AB、PD的中点. 
(1)求证:AF∥平面PCE;
(2)求证:平面PCE⊥平面PCD;
(3)求四面体PEFC的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场欲经销某种商品,考虑到不同顾客的喜好,决定同时销售A、B两个品牌,根据生产厂家营销策略,结合本地区以往经销该商品的大数据统计分析,A品牌的销售利润y1与投入资金x成正比,其关系如图1所示,B品牌的销售利润y2与投入资金x的算术平方根成正比,其关系如图2所示(利润与资金的单位:万元). 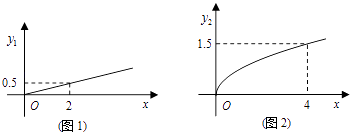
(1)分别将A、B两个品牌的销售利润y1、y2表示为投入资金x的函数关系式;
(2)该商场计划投入5万元经销该种商品,并全部投入A、B两个品牌,问:怎样分配这5万元资金,才能使经销该种商品获得最大利润,其最大利润为多少万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】函数f(x)=ka﹣x(k,a为常数,a>0且a≠1)的图象过点A(0,1),B(3,8).
(1)求函数f(x)的解析式;
(2)若函数g(x)= ![]() 是奇函数,求b的值;
是奇函数,求b的值;
(3)在(2)的条件下判断函数g(x)的单调性,并用定义证明你的结论;
(4)解不等式g(3x)+g(x﹣3﹣x2)<0.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为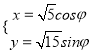 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为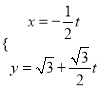 (
(![]() 为参数).以原点为极点,
为参数).以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,点
轴的正半轴为极轴建立极坐标系,点![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求点![]() 的直角坐标,并求曲线
的直角坐标,并求曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 的两个交点为
的两个交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=( ![]() )x .
)x .
(1)求函数f(x)的解析式;
(2)在所给坐标系中画出函数f(x)的图象,并根据图象写出函数f(x)的单调区间.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于实数x,符号[x]表示不超过x的最大整数,例如[π]=3,[﹣1.08]=﹣2,定义函数f(x)=x﹣[x],下列命题中正确命题的序号 .
①函数f(x)的最大值为1;
②函数f(x)的最小值为0;
③方程f(x)﹣ ![]() =0有无数个解;
=0有无数个解;
④函数f(x)是增函数;
⑤对任意的x∈R,函数f(x)满足f(x+1)=f(x);
⑥函数f(x)的图象与函数g(x)=|lgx|的图象的交点个数为10个.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数 ![]() ,a为正常数.
,a为正常数.
(1)若f(x)=lnx+φ(x),且a= ![]() ,求函数f(x)的单调增区间;
,求函数f(x)的单调增区间;
(2)在(1)中当a=0时,函数y=f(x)的图象上任意不同的两点A(x1 , y1),B(x2 , y2),线段AB的中点为C(x0 , y0),记直线AB的斜率为k,试证明:k>f'(x0).
(3)若g(x)=|lnx|+φ(x),且对任意的x1 , x2∈(0,2],x1≠x2 , 都有 ![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
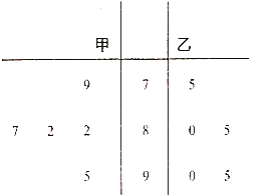
【题目】甲、乙两位学生参加某项竞赛培训,在培训期间,他们参加的5项预赛成绩的茎叶图记录如下:
(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(2)现要从中选派一人参加该项竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com