
科目: 来源: 题型:
【题目】如图,AB是圆O的直径,PB是圆O的切线,过A点作AE∥OP交圆O于E点,PA交圆O于点F,连接PE. 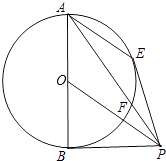
(1)求证:PE是圆O的切线;
(2)设AO=3,PB=4,求PF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】共享单车是指企业在校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是共享经济的一种新形态.一个共享单车企业在某个城市就“一天中一辆单车的平均成本(单位:元)与租用单车的数量(单位:千辆)之间的关系”进行调查研究,在调查过程中进行了统计,得出相关数据见下表:
租用单车数量 | 2 | 3 | 4 | 5 | 8 |
每天一辆车平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根据以上数据,研究人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲: ![]() ,方程乙:
,方程乙: ![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务:
①完成下表(计算结果精确到0.1)(备注: ![]() ,
,![]() 称为相应于点
称为相应于点![]() 的残差(也叫随机误差));
的残差(也叫随机误差));
租用单车数量 | 2 | 3 | 4 | 5 | 8 | |
每天一辆车平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
模型甲 | 估计值 | 2.4 | 2.1 | 1.6 | ||
残差 | 0 | -0.1 | 0.1 | |||
模型乙 | 估计值 | 2.3 | 2 | 1.9 | ||
残差 | 0.1 | 0 | 0 | |||
②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() 的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.
(2)这个公司在该城市投放共享单车后,受到广大市民的热烈欢迎,共享单车常常供不应求,于是该公司研究是否增加投放.根据市场调查,这个城市投放8千辆时,该公司平均一辆单车一天能收入10元,6元收入的概率分别为0.6,0.4;投放1万辆时,该公司平均一辆单车一天能收入10元,6元收入的概率分别为0.4,0.6.问该公司应该投放8千辆还是1万辆能获得更多利润?(按(1)中拟合效果较好的模型计算一天中一辆单车的平均成本,利润=收入-成本).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数f(x)满足f(0)=2和f(x+1)﹣f(x)=2x﹣1对任意实数x都成立.
(1)求函数f(x)的解析式;
(2)当t∈[﹣1,3]时,求y=f(2t)的值域.
查看答案和解析>>
科目: 来源: 题型:
【题目】在高中学习过程中,同学们经常这样说:“数学物理不分家,如果物理成绩好,那么学习数学就没什么问题.”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系的结论,现从该班随机抽取5名学生在一次考试中的数学和物理成绩,如下表:
编号 成绩 | 1 | 2 | 3 | 4 | 5 |
物理( | 90 | 85 | 74 | 68 | 63 |
数学( | 130 | 125 | 110 | 95 | 90 |
(1)求数学成绩![]() 对物理成绩
对物理成绩![]() 的线性回归方程
的线性回归方程![]() (
(![]() 精确到
精确到![]() ),若某位学生的物理成绩为80分,预测他的数学成绩(结果精确到个位);
),若某位学生的物理成绩为80分,预测他的数学成绩(结果精确到个位);
(2)要从抽取的这五位学生中随机选出2位参加一项知识竞赛,求选中的学生的数学成绩至少有一位高于120分的概率.
(参考公式:  ,
, ![]() .)
.)
(参考数据: ![]() ,
, ![]() .)
.)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f (x)= ![]() 的定义域为A,m>0,函数g(x)=4 x﹣1(0<x≤m)的值域为B.
的定义域为A,m>0,函数g(x)=4 x﹣1(0<x≤m)的值域为B.
(1)当m=1时,求 (R A)∩B;
(2)是否存在实数m,使得A=B?若存在,求出m的值; 若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数 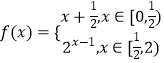 ,若存在x1 , x2 , 当0≤x1<x2<2时,f(x1)=f(x2),则x1f(x2)﹣f(x2)的取值范围为( )
,若存在x1 , x2 , 当0≤x1<x2<2时,f(x1)=f(x2),则x1f(x2)﹣f(x2)的取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
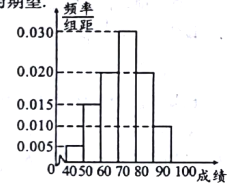
【题目】2017年《诗词大会》火爆荧屏,某校为此举办了一场主题为“爱诗词、爱祖国”的诗词知识竞赛,从参赛的全体学生中抽出60人的成绩(满分100分)作为样本.对这60名学生的成绩进行统计,并按![]() ,
, ![]() ,
, ![]() 分组,得到如图所示的频率分布直方图.
分组,得到如图所示的频率分布直方图.
(Ⅰ)若同一组数据用该组区间的中点值代表,估计参加这次知识竞赛的学生的平均成绩;
(Ⅱ)估计参加这次知识竞赛的学生成绩的中位数(结果保留一位小数);
(Ⅲ)若规定80分以上(含80分)为优秀,用频率估计概率,从全体参赛学生中随机抽取3名,记其中成绩优秀的人数为![]() ,求
,求![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】若函数f(x)=x2+a|x|+2,x∈R在区间[3,+∞)和[﹣2,﹣1]上均为增函数,则实数a的取值范围是( )
A.[﹣ ![]() ,﹣3]
,﹣3]
B.[﹣6,﹣4]
C.[﹣3,﹣2 ![]() ]
]
D.[﹣4,﹣3]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com