
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直线坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的参数方程;
的参数方程;
(2)设点![]() 在
在![]() 上,
上, ![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定义在[﹣2,2]上的函数y=f(x)和y=g(x),其图象如图所示:给出下列四个命题:
①方程f[g(x)]=0有且仅有6个根 ②方程g[f(x)]=0有且仅有3个根
③方程f[f(x)]=0有且仅有5个根 ④方程g[g(x)]=0有且仅有4个根
其中正确命题的序号( )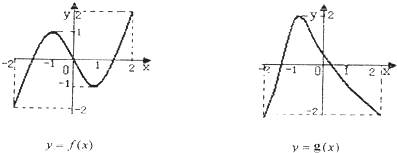
A.①②③
B.②③④
C.①②④
D.①③④
查看答案和解析>>
科目: 来源: 题型:
【题目】小明家订了一份报纸,暑假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.
(1)根据图中的数据信息,求出众数![]() 和中位数
和中位数![]() (精确到整数分钟);
(精确到整数分钟);
(2)小明的父亲上班离家的时间![]() 在上午
在上午![]() 至
至![]() 之间,而送报人每天在
之间,而送报人每天在![]() 时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件
时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件![]() )的概率.
)的概率.

查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=kax﹣a﹣x(a>0且a≠1)是定义域为R的奇函数.
(1)若f(1)>0,试求不等式f(x2+2x)+f(x﹣4)>0的解集;
(2)若f(1)= ![]() ,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值为﹣2,求m的值.
,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值为﹣2,求m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() ,圆
,圆![]() 的圆心
的圆心![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 到椭圆
到椭圆![]() 的右焦点的距离为
的右焦点的距离为![]() .
.
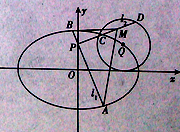
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() ,且
,且![]() 交椭圆
交椭圆![]() 于
于![]() 两点, 直线
两点, 直线![]() 交圆
交圆![]() 于
于![]() 两点, 且
两点, 且![]() 为
为![]() 的中点, 求
的中点, 求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知F1 , F2为椭圆C: ![]() (a>b>0)的左、右焦点,M为椭圆C的上顶点,且|MF1|=2,右焦点与右顶点的距离为1.
(a>b>0)的左、右焦点,M为椭圆C的上顶点,且|MF1|=2,右焦点与右顶点的距离为1.
(1)求椭圆C的标准方程;
(2)若直线l与椭圆C相交于A,B两点,且直线OA,OB的斜率kOA , kOB满足kOAkOB=﹣ ![]() ,求△AOB的面积.
,求△AOB的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】双流中学校运动会招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如图所示的茎叶图(单位: ![]() ),身高在175
),身高在175![]() 以上(包括175
以上(包括175![]() )定义为“高个子”,身高在175
)定义为“高个子”,身高在175![]() 以 下(不包括175
以 下(不包括175![]() )定义为“非高个子”.
)定义为“非高个子”.

(1)如果用分层抽样的方法从“高个子”和“非高个子”中共抽取5人,再从这5人中选2人,求至少有一人是“高个子”的概率?
(2)若从身高180![]() 以上(包括180
以上(包括180![]() )的志愿者中选出男、女各一人,求这两人身高相差5
)的志愿者中选出男、女各一人,求这两人身高相差5![]() 以上的概率.
以上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com