【题目】已知y=f（x）是偶函数，而y=f（x+1）是奇函数，且对任意0≤x≤1，都有f（x）≥0，f（x）是增函数，则a=f（2010），b=f（ ），c=﹣f（ ）的大小关系是（ ）
A.b＜c＜a
B.c＜b＜a
C.a＜c＜b
D.a＜b＜c

（1）请根据上表提供的数据，用最小二乘法求出 关于x的线性回归方程 ；
（2）我们把中（1）的线性回归方程记作模型一，观察散点图发现该组数据也可以用函数模型 =c1ln（c2x）拟合，记作模型二．经计算模型二的相关指数R2=0.64，
①请说明R2=0.64这一数据在线性回归模型中的实际意义．
②计算模型一中的R2的值（精确到0.01），通过数据说明，两种模型中哪种模型的拟合效果好．
参考公式和数值：用最小工乘法求线性回归方程系数公式 = 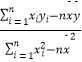， ．R2=1﹣ 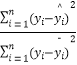， =0.651，（2×2.2+3×3.8+4×5.5+5×6.5+6×7.0=112.3）

【题目】设甲、乙、丙三人进行围棋比赛，每局两人参加，没有平局．在一局比赛中，甲胜乙的概率为 ，甲胜丙的概率为 ，乙胜丙的概率为 ．比赛顺序为：首先由甲和乙进行第一局的比赛，再由获胜者与未参加比赛的选手进行第二局的比赛，依此类推，在比赛中，有选手获胜满两局就取得比赛的胜利，比赛结束．
（1）求只进行了三局比赛，比赛就结束的概率；
（2）记从比赛开始到比赛结束所需比赛的局数为ξ，求ξ的概率分布列和数学期望Eξ．

A. B. C. D.

【题目】已知函数f（x）=x2﹣2ax+a在区间（1，3）内有极小值，则函数g（x）= 在区间（1，+∝）上一定（ ）
A.有最小值
B.有最大值
C.是减函数
D.是增函数

【题目】语文老师要从10篇课文中随机抽3篇让学生背诵，某学生只能背诵其中的6篇，求：
（1）抽到他能背诵的课文的数量的分布列；
（2）他能及格的概率．

（Ⅰ）证明：||<；

（Ⅱ）比较|1-4ab|与2|a-b|的大小，并说明理由.

【题目】已知抛物线，直线交于两点， 是的中点，过作轴的垂线交于点.

（1）证明：抛物线在点处的切线与平行；

（2）是否存在实数，使以为直径的圆经过点？若存在，求出的值；若不存在，请说明理由.

【题目】已知曲线C1的参数方程是 (φ为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程是ρ＝2.正方形ABCD的顶点都在C2上，且A，B，C，D依逆时针次序排列，点A的极坐标为.

(1)求点A，B，C，D的直角坐标；

(2)设P为C1上任意一点，求|PA|2＋|PB|2＋|PC|2＋|PD|2的取值范围．

则D（ξ）的最大值为 ．