
科目: 来源: 题型:
【题目】已知△ABC的顶点A(0,1),AB边上的中线CD所在的直线方程为2x﹣2y﹣1=0,AC边上的高BH所在直线的方程为y=0.
(1)求△ABC的顶点B、C的坐标;
(2)若圆M经过不同的三点A、B、P(m,0),且斜率为1的直线与圆M相切于点P,求圆M的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=2x+2﹣x . (Ⅰ)试写出这个函数的性质(不少于3条,不必说明理由),并作出图象;
(Ⅱ)设函数g(x)=4x+4﹣x﹣af(x),求这个函数的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】用数学归纳法证明“1+2+22+…+2n-1=2n-1(n∈N+)”的过程中,第二步n=k时等式成立,则当n=k+1时,应得到( )
A.1+2+22+…+2k-2+2k-1=2k+1-1
B.1+2+22+…+2k+2k+1=2k-1+2k+1
C.1+2+22+…+2k-1+2k+1=2k+1-1
D.1+2+22+…+2k-1+2k=2k+1-1
查看答案和解析>>
科目: 来源: 题型:
【题目】首项为正数的数列{an}满足an+1=(a+3),n∈N*.
(1)证明:若a1为奇数,则对一切n≥2,an都是奇数;
(2)若对一切n∈N*都有an+1>an , 求a1的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC,F为CE上的点,且BF⊥平面ACE. 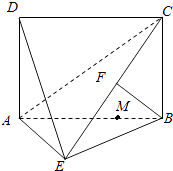
(1)求证:AE⊥BE;
(2)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一曲线C是与两个定点O(0,0),A(3,0)的距离比为 ![]() 的点的轨迹.
的点的轨迹.
(1)求曲线C的方程,并指出曲线类型;
(2)过(﹣2,2)的直线l与曲线C相交于M,N,且|MN|=2 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)函数![]() 的图象与
的图象与![]() 的图象无公共点,求实数
的图象无公共点,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)是否存在实数![]() ,使得对任意的
,使得对任意的![]() ,都有函数
,都有函数![]() 的图象在
的图象在![]() 的图象的下方?若存在,请求出整数
的图象的下方?若存在,请求出整数![]() 的最大值;若不存在,请说理由.
的最大值;若不存在,请说理由.
(参考数据:![]() ,
,![]() ,
,![]() ).
).
查看答案和解析>>
科目: 来源: 题型:
【题目】近年来空气质量逐步恶化,雾霾天气现象增多,大气污染危害加重,大气污染可引起心悸、呼吸困难等心肺疾病.为了解心肺疾病是否与性别有关,在市第一人民医院随机对入院50人进行了问卷调查,得到如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |||||||||
男 | 20 | 5 | 25 | ||||||||
女 | 10 | 15 | 25 | ||||||||
合计 | 30 | 20 | 50 | ||||||||
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | ||||
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | ||||
(1)是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由;(2)已知在患心肺疾病的10位女性中,有3位又患有胃病,现在从患心肺疾病的10位女性中,选出3位进行其他方面的排查,其中患胃病的人数为![]() ,求
,求![]() 的分布列、数学期望.参考公式:
的分布列、数学期望.参考公式:![]() ,其中
,其中![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点Pn(an , bn)满足an+1=an·bn+1 , bn+1=(n∈N*)且点P1的坐标为(1,-1).
(1)求过点P1 , P2的直线l的方程;
(2)试用数学归纳法证明:对于n∈N* , 点Pn都在(1)中的直线l上.
查看答案和解析>>
科目: 来源: 题型:
【题目】某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位女教师的概率.
附:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com