【题目】已知函数y=f（x）对任意x∈R，恒有（f（x）﹣sinx）（f（x）﹣cosx）=0成立，则下列关于函数 y=f（x）的说法正确的是（ ）
A.最小正周期是2π
B.值域是[﹣1，1]
C.是奇函数或是偶函数
D.以上都不对

已知函数f（x）＝｜x＋1｜＋｜x－3｜．

（1）若关于x的不等式f（x）＜a有解，求实数a的取值范围：

（2）若关于x的不等式f（x）＜a的解集为（b， ），求a＋b的值．

【题目】已知双曲线 的右焦点为F(c,0)．
（1）若双曲线的一条渐近线方程为y＝x且c＝2，求双曲线的方程；
（2）以原点O为圆心，c为半径作圆，该圆与双曲线在第一象限的交点为A ， 过A作圆的切线，斜率为 ，求双曲线的离心率．

【题目】如图，两个椭圆， 内部重叠区域的边界记为曲线C，P是曲线C上的任意一点，给出下列四个判断：

①P到F1（－4，0）、F2（4，0）、E1（0，－4）、E2（0，4）四点的距离之和为定值；

②曲线C关于直线y＝x、y＝－x均对称；③曲线C所围区域面积必小于36．

④曲线C总长度不大于6π．上述判断中正确命题的序号为________________．

【题目】已知抛物线E：y2=2px（p＞0）的准线与x轴交于点K，过点K作圆C：（x﹣2）2+y2=1的两条切线，切点为M，N，|MN|=
（1）求抛物线E的方程
（2）设A、B是抛物线E上分别位于x轴两侧的两个动点，且 = （其中O为坐标原点）
①求证：直线AB必过定点，并求出该定点Q的坐标
②过点Q作AB的垂线与抛物线交于G、D两点，求四边形AGBD面积的最小值．

【题目】如图，在矩形ABCD中，AB=2BC，点M在边DC上，点F在边AB上，且DF⊥AM，垂足为E，若将△ADM沿AM折起，使点D位于D′位置，连接D′B，D′C得四棱锥D′﹣ABCM．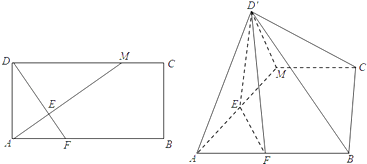

（1）求证：AM⊥D′F；
（2）若∠D′EF= ，直线D'F与平面ABCM所成角的大小为 ，求直线AD′与平面ABCM所成角的正弦值．

【题目】如图，M，N，K分别是正方体ABCD﹣A1B1C1D1的棱AB，CD，C1D1的中点．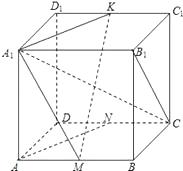

（1）求证：AN∥平面A1MK；
（2）求证：平面A1B1C⊥平面A1MK．

【题目】已知直线l经过两条直线l1：3x+4y﹣2=0与l2：2x+y+2=0的交点P．
（1）求垂直于直线l3：x﹣2y﹣1=0的直线l的方程；
（2）求与坐标轴相交于两点，且以P为中点的直线方程．

【题目】过抛物线E:x2=2py(p>0) 的焦点F作斜率分别为 k1,k2 的两条不同的直线 l1,l2 ，且k1+k2=2 ，l1与E 相交于点A，B， l2与E 相交于点C，D.以AB，CD为直径的圆M，圆N（M，N为圆心）的公共弦所在的直线记为 l .
（1）若k1>0,k2>0 ，证明；；
（2）若点M到直线 l 的距离的最小值为 ，求抛物线E的方程.

【题目】据市场调查，某种商品一年内每件出厂价在7千元的基础上，按月呈f（x）＝Asin（ωx＋）＋b （A＞0，ω＞0，｜ ｜＜）的模型波动（x为月份），已知3月份达到最高价9千元，7月份价格最低为5千元，根据以上条件可确定f（x）的解析式为

A. f（x）＝2sin（x－）＋7 （1≤x≤12，x∈N＋）

B. f（x）＝9sin（x－） （1≤x≤12，x∈N＋）

C. f（x）＝2sinx＋7 （1≤x≤12，x∈N＋）

D. f（x）＝2sin（x＋）＋7 （1≤x≤2，x∈N＋）