【题目】已知圆C的方程为：x2+y2=4
（1）求过点P（2，1）且与圆C相切的直线l的方程；
（2）直线l过点D（1，2），且与圆C交于A、B两点，若|AB|=2 ，求直线l的方程；
（3）圆C上有一动点M（x0 ， y0）， =（0，y0），若向量 = + ，求动点Q的轨迹方程．

【题目】根据下列条件，分别求直线方程：
（1）经过点A（3，0）且与直线2x+y﹣5=0垂直；
（2）求经过直线x﹣y﹣1=0与2x+y﹣2=0的交点，且平行于直线x+2y﹣3=0的直线方程．

【题目】祖暅原理也就是“等积原理”，它是由我国南北朝杰出的数学家祖冲之的儿子祖暅首先提出来的，祖暅原理的内容是：夹在两个平行平面间的两个几何体，被平行于这两个平行平面的平面所截，如果截得两个截面的面积总相等，那么这两个几何体的体积相等．已知，两个平行平面间有三个几何体，分别是三棱锥、四棱锥、圆锥（高度都为），其中：三棱锥的底面是正三角形（边长为），四棱锥的底面是有一个角为的菱形（边长为），圆锥的体积为，现用平行于这两个平行平面的平面去截三个几何体，如果截得的三个截面的面积相等，那么，下列关系式正确的是（ ）

A. B.

C. D.

【题目】已知函数f（x）=2 sin（x+ ）cos（x+ ）+sin2x+a的最大值为1．
（1）求函数f（x）的单调递增区间；
（2）将f（x）的图象向左平移 个单位，得到函数g（x）的图象，若方程g（x）=m在x∈[0， ]上有解，求实数m的取值范围．

【题目】已知p：实数x满足x2﹣4ax+3a2＜0，其中a＞0； q：实数x满足2＜x≤3．
（1）若a=1，且p∧q为真，求实数x的取值范围；
（2）若p是q的必要不充分条件，求实数a的取值范围．

【题目】正方形ABCD所在的平面与三角形CDE所在的平面交于CD，且AE⊥平面CDE．

（1）求证：AB∥平面CDE；
（2）求证：平面ABCD⊥平面ADE．

【题目】已知函数f（x）= ，若方程f（x）=a有四个不同的解x1 ， x2 ， x3 ， x4 ， 且x1＜x2＜x3＜x4 ， 则x3（x1+x2）+ 的取值范围是（ ）
A.（﹣1，+∞）
B.（﹣1，1]
C.（﹣∞，1）
D.[﹣1，1）

【题目】如图所示，E是正方形ABCD所在平面外一点，E在面ABCD上的正投影F恰在AC上，FG∥BC，AB=AE=2，∠EAB=60°，有以下四个命题：
（1）CD⊥面GEF；
（2）AG=1；
（3）以AC，AE作为邻边的平行四边形面积是8；
（4）∠EAD=60°．
其中正确命题的个数为（ ）

A.1
B.2
C.3
D.4

【题目】如图，正方形O′A′B′C′的边长为1cm，它是水平放置的一个平面图形的直观图，则原图的周长是（ ）

A.8cm
B.6cm
C.2（1+ ）cm
D.2（1+ ）cm

【题目】如图，在四棱锥P﹣ABCD中，PA⊥底面ABCD，BC⊥PB，△BCD为等边三角形，PA=BD= ，AB=AD，E为PC的中点．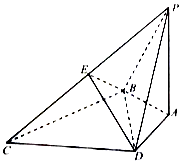

（1）求证：BC⊥AB；
（2）求AB的长；
（3）求平面BDE与平面ABP所成二面角的正弦值．