【题目】某学校高三年级有学生500人，其中男生300人，女生200人，为了研究学生的数学成绩是否与性别有关，现采用分层抽样的方法，从中抽取了100名学生，先统计了他们期中考试的数学分数，然后按性别分为男、女两组，再将两组学生的分数分成5组：[100，110），[110，120），[120，130），[130，140），[140，150]分别加以统计，得到如图所示的频率分布直方图．
附：K2= ．
（1）从样本中分数小于110分的学生中随机抽取2人，求两人恰好为一男一女的概率；
（2）若规定分数不小于130分的学生为“数学尖子生”，请你根据已知条件完成2×2列联表，并判断是否有90%的把握认为“数学尖子生与性别有关”？

【题目】已知椭圆C： =1（a＞b＞0）上的动点到焦点距离的最小值为 -1．以原点为圆心、椭圆的短半轴长为半径的圆与直线x﹣y+ =0相切．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若过点M（2，0）的直线与椭圆C相交于A，B两点，P为椭圆上一点，且满足 + =t （O为坐标原点）．当|AB|= 时，求实数t的值．

【题目】在四边形ABCD中，已知 ∥ ， =（6，1）， =（x，y）， =（﹣2，﹣3）．
（1）求用x表示y的关系式；
（2）若 ⊥ ，求x、y值．

【题目】已知 ， 的夹角为60°， ， ，当实数k为何值时，
（1）
（2） ．

【题目】若命题p：曲线 =1为双曲线，命题q：函数f（x）=（4﹣a）x在R上是增函数，且p∨q为真命题，p∧q为假命题，则实数a的取值范围是 ．

【题目】某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的300天内，西红柿场售价与上市时间的关系如图一的一条折线表示；西红柿的种植成本与上市时间的关系如图二的抛物线段表示．

（1）写出图一表示的市场售价与时间的函数关系式p=f（t）；写出图二表示的种植成本与时间的函数关系式Q=g（t）；
（2）认定市场售价减去种植成本为纯收益，问何时上市的西红柿纯收益最大？（注：市场售价各种植成本的单位：元/102㎏，时间单位：天）

【题目】已知0＜a＜1，函数f（x）=loga（ax﹣1）
（I）求函数f（x）的定义域；
（Ⅱ）判断f（x）的单调性；
（Ⅲ）若m满足f（1﹣m）≥f（1﹣m2），求m的范围．

（1）若m=2，求A∩B；

（2）若BA，求实数m的取值范围．

【题目】如图所示，在四棱锥P﹣ABCD中，底面ABCD是棱长为2的正方形，侧面PAD为正三角形，且面PAD⊥面ABCD，E、F分别为棱AB、PC的中点．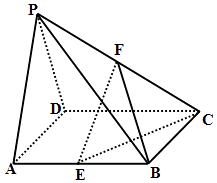
（1）求证：EF∥平面PAD；
（2）求三棱锥B﹣EFC的体积；
（3）求二面角P﹣EC﹣D的正切值．

（1）求f（x）；

（2）设 ，m＞0，求函数g（x）在[0，m]上的最大值；

（3）设h（x）=lnf（x），若对于一切x∈[0，1]，不等式h（x+1﹣t）＜h（2x+2）恒成立，求实数t的取值范围．