
科目: 来源: 题型:
【题目】下表是某厂的产量x与成本y的一组数据:
产量x(千件) | 2 | 3 | 5 | 6 |
成本y(万元) | 7 | 8 | 9 | 12 |
(Ⅰ)根据表中数据,求出回归直线的方程 ![]() =
= ![]() x
x ![]() (其中
(其中 ![]() =
= 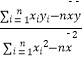 ,
, ![]() =
= ![]() ﹣
﹣ ![]() )
)
(Ⅱ)预计产量为8千件时的成本.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax2+(2﹣a)x. (Ⅰ)讨论f(x)的单调性;
(Ⅱ)设a>0,证明:当0<x< ![]() 时,f(
时,f( ![]() +x)>f(
+x)>f( ![]() ﹣x);
﹣x);
(Ⅲ)若函数y=f(x)的图象与x轴交于A,B两点,线段AB中点的横坐标为x0 , 证明:f′(x0)<0.
查看答案和解析>>
科目: 来源: 题型:
【题目】2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图: (I)为了了解部分市民对“共享单车”评分较低的原因,该部门从评分低于60分的市民中随机抽取2人进行座谈,求这2人评分恰好都在[50,60)的概率;
(II)根据你所学的统计知识,判断该项目能否通过考核,并说明理由.
(注:满意指数= ![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ax4lnx+bx4﹣c在x=1处取得极值﹣3﹣c.
(1)试求实数a,b的值;
(2)试求函数f(x)的单调区间;
(3)若对任意x>0,不等式f(x)≥﹣2c2恒成立,求实数c的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】给出下列不等式:①x≥ln(x+1)(x>﹣1)② ![]() >﹣
>﹣ ![]() +2x﹣
+2x﹣ ![]() (x>0)③ln
(x>0)③ln ![]() >2(x+
>2(x+ ![]() )(x∈(0,1))其中成立的个数是( )
)(x∈(0,1))其中成立的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线l:kx﹣y+1+2k=0(k∈R) (Ⅰ)证明直线l经过定点并求此点的坐标;
(Ⅱ)若直线l不经过第四象限,求k的取值范围;
(Ⅲ)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设△AOB的面积为S,求S的最小值及此时直线l的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知a,b是实数,函数f(x)=x|x﹣a|+b.
(1)当a=2时,求函数f(x)的单调区间;
(2)当a>0时,求函数f(x)在区间[1,2]上的最大值;
(3)若存在a∈[﹣3,0],使得函数f(x)在[﹣4,5]上恒有三个零点,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com