【题目】我国古代数学著作《九章算术》有如下问题：“今有蒲（水生植物名）生一日，长三尺；莞（植物名，俗称水葱、席子草）生一日，长一尺．蒲生日自半，莞生日自倍．问几何日而长等？”意思是：今有蒲生长1日，长为3尺；莞生长1日，长为1尺．蒲的生长逐日减半，莞的生长逐日增加1倍．若蒲、莞长度相等，则所需的时间约为（ ）（结果保留一位小数．参考数据：，）（ ）

A. 1.3日 B. 1.5日 C. 2.6日 D. 2.8日

【题目】在四棱锥中，底面是矩形， 平面， ，以的中点为球心， 为直径的球面交于点，交于点.

（1）求证：平面平面；

（2）求点到平面的距离.

【题目】执行如图所示的程序框图，则输出的k的值为（ ）

A.7
B.6
C.5
D.4

【题目】若是公差不为0的等差数列的前项和，且成等比数列，.

（1）求数列的通项公式；

（2）设是数列的前项和，求使得对所有都成立的最小正整数.

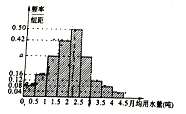
【题目】我国是世界上严重缺水的国家，某市为了制定合理的节水方案，对居民用水情况进行调查，通过抽样，获得某年100为居民每人的月均用水量（单位：吨），将数据按照分成9组，制成了如图所示的频率分布直方图.

（1）求直方图的的值；

（2）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，说明理由.

（3）估计居民月用水量的中位数.

【题目】已知，若关于的方程恰好有 4 个不相等的实数解，则实数的取值范围为（ ）

A. B. C. D.

【题目】已知椭圆E： =1（a＞b＞0）上任意一点到两焦点距离之和为 ，离心率为 ，左、右焦点分别为F1 ， F2 ， 点P是右准线上任意一点，过F2作直线PF2的垂线F2Q交椭圆于Q点．
（1）求椭圆E的标准方程；
（2）证明：直线PQ与直线OQ的斜率之积是定值；
（3）证明：直线PQ与椭圆E只有一个公共点．

【题目】请认真阅读下列程序框图，然后回答问题，其中n0∈N．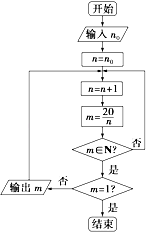
（1）若输入n0=0，写出所输出的结果；
（2）若输出的结果中有5，求输入的自然数n0的所有可能的值；
（3）若输出的结果中，只有三个自然数，求输入的自然数n0的所有可能的值．

【题目】已知集合A={x|3≤3x≤27}， ．
（1）分别求A∩B，（RB）∪A；
（2）已知集合C={x|1＜x＜a}，若CA，求实数a的取值集合．

【题目】刘徽（约公元 225 年—295 年）是魏晋时期伟大的数学家，中国古典数学理论的奠基人之一，他的杰作《九章算术注》和《海岛算经》是中国宝贵的古代数学遗产. 《九章算术·商功》中有这样一段话：“斜解立方，得两壍堵. 斜解壍堵，其一为阳马，一为鳖臑.” 刘徽注：“此术臑者，背节也，或曰半阳马，其形有似鳖肘，故以名云.” 其实这里所谓的“鳖臑（biē nào）”，就是在对长方体进行分割时所产生的四个面都为直角三角形的三棱锥. 如图，在三棱锥中， 垂直于平面， 垂直于，且 ，则三棱锥的外接球的球面面积为__________.