【题目】以直角坐标系的原点O为极点，x轴的正半轴为极轴建立极坐标系．
（1）将直线l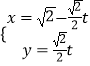： （t为参数）化为极坐标方程；
（2）设P是（1）中直线l上的动点，定点A（ ， ），B是曲线ρ=﹣2sinθ上的动点，求|PA|+|PB|的最小值．

【题目】已知0＜a＜1，函数f（x）=logax．
（1）若f（5a﹣1）≥f（2a），求实数a的最大值；
（2）当a= 时，设g（x）=f（x）﹣3x+2m，若函数g（x）在（1，2）上有零点，求实数m的取值范围．

【题目】设函数f（x）=ln（x+1）+a（x2﹣x），a≥0．
（1）当a=1时，求函数f（x）的极值；
（2）若x＞0，f（x）≥0成立，求a的取值范围．

该小组的研究方案是：先从这六组数据中选取6日和11日的两组数据作为检验数据，用剩下的4组数据即：7日至10日的四组数据求出线性回归方程．
（1）请按研究方案求出y关于x的线性回归方程 = x+ ；
（2）用6日和11日的两组数据作为检验数据，并判断该小组所得线性回归方程是否理想．（若由线性回归方程得到的估计数据与所选的检验数据的误差不超过1mm，则认为该方程是理想的）
参考公式： ．

【题目】已知抛物线C：y2=2px（p＞0）
（1）若直线x﹣y﹣2=0过抛物线C的焦点，求抛物线C的方程，并求出准线方程；
（2）设p=2，A，B是C上异于坐标原点O的两个动点，满足OA⊥OB，△ABO的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．

（1）根据表中数据，问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”；
（2）已知在被调查的北方学生中有5名数学系的学生，其中2名喜欢甜品，现在从这5名学生中随机抽取3人，求至多有1人喜欢甜品的概率． 附：K2=

【题目】已知函数f（x）=2x2+（2﹣m）x﹣m，g（x）=x2﹣x+2m．
（1）若m=1，求不等式f（x）＞0的解集；
（2）若m＞0，求关于x的不等式f（x）≤g（x）的解集．

【题目】已知样本数据a1 ， a2 ， a3 ， a4 ， a5的方差s2= （a12+a22+a32+a42+a52﹣80），则样本数据2a1+1，2a2+1，2a3+1，2a4+1，2a5+1的平均数为 ．

【题目】甲乙两位同学进行乒乓球比赛，甲获胜的概率为0.4，现采用随机模拟的方法估计这两位同学打3局比赛甲恰好获胜2局的概率：先利用计算器产生0到9之间取整数值的随机数，制定1，2，3，4表示甲获胜，用5，6，7，8，9，0表示乙获胜，再以每三个随机数为一组，代表3局比赛的结果，经随机模拟产生了30组随机数
102 231 146 027 590 763 245 207 310 386 350 481 337 286 139
579 684 487 370 175 772 235 246 487 569 047 008 341 287 114
据此估计，这两位同学打3局比赛甲恰好获胜2局的概率为（ ）
A.
B.
C.
D.

【题目】从某工厂生产的P，Q两种型号的玻璃种分别随机抽取8个样品进行检查，对其硬度系数进行统计，统计数据用茎叶图表示（如图所示），则P组数据的众数和Q组数据的中位数分别为（ ）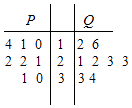

A.22和22.5
B.21.5和23
C.22和22
D.21.5和22.5