
科目: 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>0)的焦点在x轴上,且椭圆C的焦距为2. (Ⅰ)求椭圆C的标准方程;
=1(a>0)的焦点在x轴上,且椭圆C的焦距为2. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点R(4,0)的直线l与椭圆C交于两点P,Q,过P作PN⊥x轴且与椭圆C交于另一点N,F为椭圆C的右焦点,求证:三点N,F,Q在同一条直线上.
查看答案和解析>>
科目: 来源: 题型:
【题目】函数f(x)=![]() 是定义在[-l,1]上的奇函数,且f(
是定义在[-l,1]上的奇函数,且f(![]() )=
)=![]() 。
。
(1)确定函数f(x)的解析式;
(2)判断并用定义证明f(x)在(-1,1)上的单调性;
(3)若f(1-3m)+f(1+m)≥0,求实数m的所有可能的取值。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数f(x)满足f(-x-1)=f(x-1),其图象过点(0,1),且与x轴有唯一交点。
(1)求f(x)的解析式;
(2)设函数g(x)=f(x)-(2+a)x,求g(x)在[1,2]上的最小值h(a)。
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司为确定下一年投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年利润y(单位:万元)的影响,对近5年的宣传费xi和年利润yi(i=1,2,3,4,5)进行了统计,列出了下表:
x(单位:千元) | 2 | 4 | 7 | 17 | 30 |
y(单位:万元) | 1 | 2 | 3 | 4 | 5 |
员工小王和小李分别提供了不同的方案.
(1)小王准备用线性回归模型拟合y与x的关系,请你建立y关于x的线性回归方程(系数精确到0.01);
(2)小李决定选择对数回归模拟拟合y与x的关系,得到了回归方程: ![]() =1.450lnx+0.024,并提供了相关指数R2=0.995,请用相关指数说明选择哪个模型更合适,并预测年宣传费为4万元的年利润(精确到0.01)(小王也提供了他的分析数据
=1.450lnx+0.024,并提供了相关指数R2=0.995,请用相关指数说明选择哪个模型更合适,并预测年宣传费为4万元的年利润(精确到0.01)(小王也提供了他的分析数据 ![]() (yi﹣
(yi﹣ ![]() i)2=1.15) 参考公式:相关指数R2=1﹣
i)2=1.15) 参考公式:相关指数R2=1﹣ 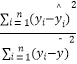
回归方程 ![]() =
= ![]() x+
x+ ![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为 ![]() =
= 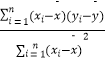 ,
, ![]() =
= ![]() ﹣
﹣ ![]() x,参考数据:ln40=3.688,
x,参考数据:ln40=3.688, ![]() =538.
=538.
查看答案和解析>>
科目: 来源: 题型:
【题目】某食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系t=![]() 且该食品在4℃的保鲜时间是16小时。已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示。给出以下四个结论:
且该食品在4℃的保鲜时间是16小时。已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示。给出以下四个结论:
①该食品在6℃的保鲜时间是8小时;
②当x∈[-6,6]时,该食品的保鲜时间t随着x增大而逐渐减少;
③到了此日13时,甲所购买的食品还在保鲜时间内;
④到了此日14时,甲所购买的食品已然过了保鲜时间。
其中,所有正确结论的序号是__________。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)判断函数![]() 的奇偶性,并给出证明;
的奇偶性,并给出证明;
(2)解不等式: ![]() ;
;
(3)若函数![]() 在
在![]() 上单调递减,比较f(2)+f(4)+…+f(2n)与2n(n∈N*)的大小关系,并说明理由.
上单调递减,比较f(2)+f(4)+…+f(2n)与2n(n∈N*)的大小关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() )
)
(1)若在区间[0,1]上有最大值1和最小值-2.求a,b的值;
(2)在(1)条件下,若在区间![]() 上,不等式f(x)
上,不等式f(x)![]()
![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在底面为平行四边形的四棱锥P﹣ABCD中,PA⊥平面ABCD,且BC=2AB═4,∠ABC=60°,点E是PD的中点. 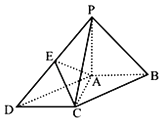
(1)求证:AC⊥PB;
(2)当二面角E﹣AC﹣D的大小为45°时,求AP的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】设命题p:直线mx﹣y+1=0与圆(x﹣2)2+y2=4有公共点;设命题q:实数m满足方程 ![]() +
+ ![]() =1表示双曲线.
=1表示双曲线.
(1)若“p∧q”为真命题,求实数m的取值范围;
(2)若“p∧q”为假命题,“p∨q”为真命题,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com