
科目: 来源: 题型:
【题目】在实数集R中定义一种运算“*”,对任意给定的a,b∈R,a*b为唯一确定的实数,且具有性质: ⑴对任意a,b∈R,a*b=b*a;(2)对任意a∈R,a*0=a;(3)对任意a,b∈R,(a*b)*c=c*(ab)+(a*c)+(c*b)﹣2c.关于函数f(x)=(3x)* ![]() 的性质,有如下说法:
的性质,有如下说法:
①函数f(x)的最小值为3;
②函数f(x)为奇函数;
③函数f(x)的单调递增区间为(﹣∞,﹣ ![]() ),(
),( ![]() ,+∞).
,+∞).
其中所有正确说法的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目: 来源: 题型:
【题目】有一种新型的洗衣液,去污速度特别快.已知每投放![]() (
(![]() 且
且![]() )个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度
)个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (分钟) 变化的函数关系式近似为
(分钟) 变化的函数关系式近似为![]() ,其中
,其中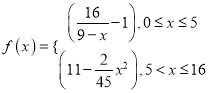 .根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
(1)若投放![]() 个单位的洗衣液,3分钟时水中洗衣液的浓度为4 (克/升),求
个单位的洗衣液,3分钟时水中洗衣液的浓度为4 (克/升),求![]() 的值;
的值;
(2)若投放4个单位的洗衣液,则有效去污时间可达几分钟?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()
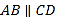
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=lnx.
(1)设h(x)为偶函数,当x<0时,h(x)=f(﹣x)+2x,求曲线y=h(x)在点(1,﹣2)处的切线方程;
(2)设g(x)=f(x)﹣mx,求函数g(x)的极值;
(3)若存在x0>1,当x∈(1,x0)时,恒有f(x)> ![]() 成立,求实数k的取值范围.
成立,求实数k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() 及圆
及圆![]() .
.
(1)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,当
两点,当![]() 时,求以线段
时,求以线段![]() 为直径的圆
为直径的圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,是否存在实数
两点,是否存在实数![]() ,使得过点
,使得过点![]() 的直线
的直线![]() 垂直平分弦
垂直平分弦![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=loga ![]() (a>0且a≠1)是奇函数.
(a>0且a≠1)是奇函数.
(1)求实数m的值;
(2)判断函数f(x)在区间(1,+∞)上的单调性并说明理由;
(3)当x∈(n,a﹣2)时,函数f(x)的值域为(1,+∞),求实数n,a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】生产某种产品的年固定成本为250万元,每生产x千件,需要另投入成本为C(x),当年产量不足80千件时,C(x)= ![]() +20x(万元),当年产量不小于80千件时,C(x)=51x+
+20x(万元),当年产量不小于80千件时,C(x)=51x+ ![]() ﹣1450(万元),通过市场分析,每件商品售价为0.05万元时,该商品能全部售完.
﹣1450(万元),通过市场分析,每件商品售价为0.05万元时,该商品能全部售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式(利润=销售额﹣成本);
(2)年产量为多少千件时,生产该商品获得的利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com