
科目: 来源: 题型:
【题目】已知各项均为正数的数列![]() 满足
满足![]() , 且
, 且![]() ,其中
,其中![]() .
.
(1) 求数列![]() 的通项公式;
的通项公式;
(2) 设数列{bn}满足 bn=![]() ,是否存在正整数
,是否存在正整数![]() ,使得b1,bm,bn成等比数列?若存在,求出所有的
,使得b1,bm,bn成等比数列?若存在,求出所有的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3) 令![]() ,记数列{cn}的前
,记数列{cn}的前![]() 项和为
项和为![]() ,其中
,其中![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系 ![]() 中,曲线
中,曲线 ![]() 的参数方程为
的参数方程为 ![]() (其中
(其中 ![]() 为参数),曲线
为参数),曲线 ![]() :
: ![]() ,以坐标原点
,以坐标原点 ![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线 ![]() 的普通方程和曲线
的普通方程和曲线 ![]() 的极坐标方程;
的极坐标方程;
(2)若射线 ![]() (
( ![]() )与曲线
)与曲线 ![]() ,
, ![]() 分别交于
分别交于 ![]() ,
, ![]() 两点,求
两点,求 ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】新生儿Apgar评分,即阿氏评分是对新生儿出生后总体状况的一个评估,主要从呼吸、心率、反射、肤色、肌张力这几个方面评分,满10分者为正常新生儿,评分7分以下的新生儿考虑患有轻度窒息,评分在4分以下考虑患有重度窒息,大部分新生儿的评分多在7-10分之间,某市级医院妇产科对1月份出生的新生儿随机抽取了16名,以下表格记录了他们的评分情况.
(1)现从16名新生儿中随机抽取3名,求至多有1名评分不低于9分的概率;
(2)以这16名新生儿数据来估计本年度的总体数据,若从本市本年度新生儿任选3名,记 ![]() 表示抽到评分不低于9分的新生儿数,求
表示抽到评分不低于9分的新生儿数,求 ![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】拖延症总是表现在各种小事上,但日积月累,特别影响个人发展.某校的一个社会实践调查小组,在对该校学生进行“是否有明显拖延症”的调查中,随机发放了110份问卷.对收回的100份有效问卷进行统计,得到如下 ![]() 列联表:
列联表:
(1)按女生是否有明显拖延症进行分层,已经从40份女生问卷中抽取了8份问卷,现从这8份问卷中再随机抽取3份,并记其中无明显拖延症的问卷的份数为 ![]() ,试求随机变量
,试求随机变量 ![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若在犯错误的概率不超过 ![]() 的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的
的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的 ![]() 的值应为多少?请说明理由.附:独立性检验统计量
的值应为多少?请说明理由.附:独立性检验统计量 ![]() ,其中
,其中 ![]() .
.
独立性检验临界值表:
查看答案和解析>>
科目: 来源: 题型:
【题目】在如图所示的多面体ABCDEF中,四边形ABCD为正方形,底面ABFE为直角梯形,∠ABF为直角, ![]() , 平面ABCD⊥平面ABFE.
, 平面ABCD⊥平面ABFE.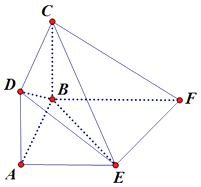
(1)求证:DB⊥EC;
(2)若AE=AB,求二面角C﹣EF﹣B的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租时间不超过两小时免费,超过两个小时的部分每小时收费2元(不足1小时的部分按1小时计算).有甲、乙两人独立来该租车点骑游(各组一车一次).设甲、乙不超过两小时还车的概率分别为 ![]() ,
, ![]() ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为 ![]() ,
, ![]() ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.
(1)求甲、乙两人所付租车费用相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量 ![]() ,求
,求 ![]() 的分布列.
的分布列.
查看答案和解析>>
科目: 来源: 题型:
【题目】等差数列{an}的前n项和为Sn , 数列{bn}是等比数列,满足a1=3,b1=1,b2+S2=10,a5﹣2b2=a3 .
(1)求数列{an}和{bn}的通项公式;
(2)令cn=anbn , 设数列{cn}的前n项和为Tn , 求Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com