【题目】某礼品店要制作一批长方体包装盒，材料是边长为的正方形纸板．如图所示，先在其中相邻两个角处各切去一个边长是的正方形，然后在余下两个角处各切去一个长、宽分别为、的矩形，再将剩余部分沿图中的虚线折起，做成一个有盖的长方体包装盒．

(1)求包装盒的容积关于的函数表达式，并求函数的定义域；

(2)当为多少时，包装盒的容积最大？最大容积是多少？

(1)p:|x|=|y|,q:x=y;

(2)p:△ABC是直角三角形,q:△ABC是等腰三角形;

(3)p:四边形的对角线互相平分,q:四边形是矩形;

(4)p:圆x2+y2=r2(r>0)与直线ax+by+c=0相切,q:c2=(a2+b2)r2.

【题目】如图，三棱柱ABC﹣A1B1C1中，CA=CB，AB=AA1 ， ∠BAA1=60°．

（1）证明：AB⊥A1C；
（2）若AB=CB=2，A1C= ，求二面角B﹣AC﹣A1的余弦值．

【题目】已知函数

（1）若且函数的值域为,求的表达式;

（2）在（1）的条件下, 当时, 是单调函数, 求实数k的取值范围;

（3）设, 且为偶函数, 判断＋能否大于零?请说明理由.

【题目】如图，将边长为2，有一个锐角为60°的菱形ABCD，沿着较短的对角线BD对折，使得，O为BD的中点.

（Ⅰ）求证：

（Ⅱ）求三棱锥的体积；

（Ⅲ）求二面角A-BC-D的余弦值.

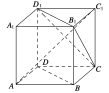
【题目】如图所示，为正方体，给出以下五个结论：

① 平面；

② ⊥平面；

③ 与底面所成角的正切值是；

④ 二面角的正切值是；

⑤ 过点且与异面直线 和 均成70°角的直线有4条．

其中，所有正确结论的序号为________．

(1)求频率分布直方图中x的值；

(2)设位于第六组的工人为拔尖工，位于第五组的工人为熟练工，现用分层抽样的方法在这两类工人中抽取一个容量为6的样本，从样本中任意取两个，求至少有一个拔尖工的概率．

【题目】已知正三角形ABC的边长为2，D、E、F分别是BC、CA、AB的中点．
（1）在三角形内部随机取一点P，求满足|PB|≥1且|PC|≥1的概率；
（2）在A、B、C、D、E、F这6点中任选3点，记这3点围成图形的面积为ξ，求随机变量ξ的分布列与数学期望Eξ．

【题目】如图，已知圆： ，点.

（1）求经过点且与圆相切的直线的方程；

（2）过点的直线与圆相交于、两点， 为线段的中点，求线段长度的取值范围.