
科目: 来源: 题型:
【题目】(选修4-4 坐标系与参数方程) 以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,设曲线C的参数方程为
轴的正半轴为极轴建立极坐标系,设曲线C的参数方程为 (
(![]() 是参数),直线
是参数),直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程和曲线C的普通方程;
的直角坐标方程和曲线C的普通方程;
(2)设点P为曲线C上任意一点,求点P到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}的各项都大于1,且a1=2,a ![]() ﹣an+1﹣a
﹣an+1﹣a ![]() +1=0(n∈N*).
+1=0(n∈N*).
(1)求证: ![]() ≤an<an+1≤n+2;
≤an<an+1≤n+2;
(2)求证: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() <1.
<1.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国古代数学著作《九章算术》中有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问:米几何?”如图所示的是解决该问题的程序框图,执行该程序框图,若输出的![]() (单位:升),则输入
(单位:升),则输入![]() 的值为( )
的值为( )

A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)经过点P(﹣2,0)与点(1,1).
=1(a>b>0)经过点P(﹣2,0)与点(1,1).
(1)求椭圆的方程;
(2)过P点作两条互相垂直的直线PA,PB,交椭圆于A,B.
①证明直线AB经过定点;
②求△ABP面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知f(x)=x2﹣a|x﹣1|+b(a>0,b>﹣1)
(1)若b=0,a>2,求f(x)在区间[0,2]内的最小值m(a);
(2)若f(x)在区间[0,2]内不同的零点恰有两个,且落在区间[0,1),(1,2]内各一个,求a﹣b的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是直角梯形,∠ABC=∠BCD= ![]() ,AB=BC=1,CD=2,PA⊥平面ABCD,E是PD的中点.
,AB=BC=1,CD=2,PA⊥平面ABCD,E是PD的中点. 
(1)求证:AE∥平面PBC;
(2)若直线AE与直线BC所成角等于 ![]() ,求二面角D﹣PB﹣A平面角的余弦值.
,求二面角D﹣PB﹣A平面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司为了了解某地区电视观众对某类体育节目的收视情况随机抽取了100名观众进行调查,其中女性有55名.如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图.将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
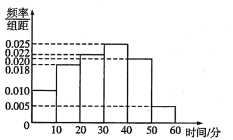
(1)根据已知条件完成下面的![]() 列联表,并据此资料你是否认为“体育迷”与性别有关?
列联表,并据此资料你是否认为“体育迷”与性别有关?
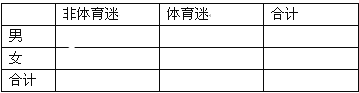
(2)将日均收看该体育节目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力.每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训.已知参加过财会培训的有60%,参加过计算机培训的有75%,假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(1)任选1名下岗人员,求该人参加过培训的概率;
(2)任选3名下岗人员,记ξ为3人中参加过培训的人数,求ξ的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com