【题目】如图，在多面体ABCDE中，DB⊥平面ABC，AE∥DB，且△ABC是边长为2的等边三角形，2AE=BD=2．
（Ⅰ）若F是线段CD的中点，证明：EF⊥面DBC；
（Ⅱ）求二面角D﹣EC﹣B的平面角的余弦值．

(1)求总决赛中获得门票总收入恰好为150万元且甲获得总冠军的概率；

(2)设总决赛中获得的门票总收入为，求的分布列和数学期望．

【题目】假设关于某种设备的使用年限 (年)与所支出的维修费用 (万元)有如下统计资料：

已知， .

，

(1)求， ；

(2)若 与具有线性相关关系，求出线性回归方程；

(3)估计使用年限为10年时，维修费用约是多少？

A. 有67.06%的把握认为A与B有关系 B. 有99%的把握认为A与B有关系

C. 有0.010的把握认为A与B有关系 D. 没有充分理由说明A与B有关系

【题目】已知函数f（x）=lnx+ ax2﹣2bx
（1）设点a=﹣3，b=1，求f（x）的最大值；
（2）当a=0，b=﹣ 时，方程2mf（x）=x2有唯一实数解，求正数m的取值范围．

【题目】甲乙两人进行围棋比赛，约定先连胜两局者直接赢得比赛.若赛完5局仍未出现连胜，则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为，乙获胜的概率为，各局比赛结果相互独立.

(1)求甲在4局以内（含4局）赢得比赛的概率；

(2)记X为比赛决出胜负时的总局数，求X的分布列和数学期望.

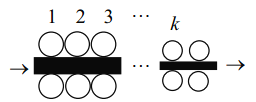
一对对轧辊的减薄率.

（1）输入钢带的厚度为，输出钢带的厚度为，若每对轧辊的减薄率不超过，问冷轧机至少需要安装几对轧辊？

（2）已知一台冷轧机共有4对减薄率为的轧辊，所有轧辊周长均为，若第对轧辊有缺陷，每滚动一周在刚带上压出一个疵点，在冷轧机输出的刚带上，疵点的间距为，易知，为了便于检修，请计算，，.

(1)求p；

(2)若这台机器一周5个工作日不发生故障，可获利5万元；发生一次故障任可获利2.5万元；发生2次故障的利润为0元；发生3次或3次以上故障要亏损1万元.这台机器一周内可能获利的均值是多少？

【题目】已知函数f（x）= sinωxcosωx﹣cos2ωx﹣ （ω＞0，x∈R）的图象上相邻两个最高点的距离为π．
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）若△ABC三个内角A、B、C的对边分别为a、b、c，且c= ，f（C）=0，sinB=3sinA，求a，b的值．

（1）求选出的3名同学是来自互不相同学院的概率；

（2）设为选出的3名同学中女同学的人数，求随机变量的分布列和数学期望．