
科目: 来源: 题型:
【题目】有3名男生,4名女生,在下列不同要求下,求不同的排列方法总数(用数字作答).
(1)全体排成一行,其中男生甲不在最左边;
(2)全体排成一行,其中4名女生必须排在一起;
(3)全体排成一行,3名男生两两不相邻.
查看答案和解析>>
科目: 来源: 题型:
【题目】以下有四种说法,其中正确说法的个数为:
(1)命题“若am2<bm2”,则“a<b”的逆命题是真命题
(2)“a>b”是“a2>b2”的充要条件;
(3) “x=3”是“x2-2x-3=0”的必要不充分条件;
(4)“![]() ”是“
”是“![]() ”的必要不充分条件.
”的必要不充分条件.
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目: 来源: 题型:
【题目】已知集合M={(x,y)|f(x,y)=0},若对任意P1(x1 , y1)∈M,均不存在P2(x2 , y2)∈M使得x1x2+y1y2=0成立,则称集合M为“好集合”,下列集合为“好集合”的是( )
A.M={(x,y)|y﹣lnx=0}
B.M={(x,y)|y﹣![]() x2﹣1=0}
x2﹣1=0}
C.M={(x,y)|(x﹣2)2+y2﹣2=0}
D.M={(x,y)|x2﹣2y2﹣1=0}
查看答案和解析>>
科目: 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 4.5 |
(Ⅰ)在给定的坐标系中画出表中数据的散点图;

(Ⅱ)试对![]() 与
与![]() 的关系进行相关性检验,如
的关系进行相关性检验,如![]() 与
与![]() 具有线性相关关系,求出
具有线性相关关系,求出![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(Ⅲ)试预测加工![]() 个零件需要多少时间?
个零件需要多少时间?
参考数据:![]() ,
,![]() .
.
附: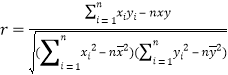 );
); ,
, ![]() ;
;
相关性检验的临界值表
n-2 | 小概率 | n-2 | 小概率 | n-2 | 小概率 | |||
0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | |||
1 | 0.997 | 1 | 4 | 0.811 | 0.917 | 7 | 0.666 | 0.798 |
2 | 0.950 | 0.990 | 5 | 0.754 | 0.874 | 8 | 0.632 | 0.765 |
3 | 0.878 | 0.959 | 6 | 0.707 | 0.834 | 9 | 0.602 | 0.735 |
注:表中的n为数据的组数
查看答案和解析>>
科目: 来源: 题型:
【题目】直线l:y=kx+1与圆O:x2+y2=1相交于A,B 两点,则“k=1”是“△OAB的面积为 ![]() ”的( )
”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分又不必要条件
查看答案和解析>>
科目: 来源: 题型:
【题目】为了调查某校高二同学是否需要学校提供学法指导,用简单随机抽样方法从该校高二年级调查了55位同学,结果如下:
男 | 女 | |
需要 | 20 | 10 |
不需要 | 10 | 15 |
(Ⅰ)估计该校高二年级同学中,需要学校提供学法指导的同学的比例(用百分数表示,保留两位有效数字);
(Ⅱ)能否有95%的把握认为该校高二年级同学是否需要学校提供学法指导与性别有关?
(Ⅲ)根据(Ⅱ)的结论,能否提出更好的调查方法来估计该校高二年级同学中,需要学校提供学法指导?说明理由.
附:![]()
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面几何中,与三角形的三条边所在直线的距离相等的点有且只有四个.类似的:在立体几何中,与正四面体的六条棱所在直线的距离相等的点 ( )
A. 有且只有一个 B. 有且只有三个 C. 有且只有四个 D. 有且只有五个
查看答案和解析>>
科目: 来源: 题型:
【题目】商家生产一种产品,需要先进行市场调研,计划对北京、上海、广州三地进行市场调研,待调研结束后决定生产的产品数量,下列四种方案中最可取的是( )
A. ![]()
B. 
C. 
D. 
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x﹣1.
(1)求f(3)+f(﹣1);
(2)求f(x)在R上的解析式;
(3)求不等式﹣7≤f(x)≤3的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com