
科目: 来源: 题型:
【题目】潮州统计局就某地居民的月收入调查了![]() 人,并根据所得数据画了样本的频率分
人,并根据所得数据画了样本的频率分
布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在![]() )。
)。

(1)求居民月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这![]() 人中分层抽样方法抽出
人中分层抽样方法抽出![]() 人作进一步分析,则月收入在
人作进一步分析,则月收入在![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解篮球爱好者小张的投篮命中率与打篮球时间之间的关系,下表记录了小张某月1号到5号每天打篮球时间![]() (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率![]() 之间的关系:
之间的关系:
时间 | 1 | 2 | 3 | 4 | 5 |
命中率 | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
(1)求小张这![]() 天的平均投篮命中率;
天的平均投篮命中率;
(2)利用所给数据求小张每天打篮球时间![]() (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率![]() 之间的线性回归方程
之间的线性回归方程![]() ;(参考公式:
;(参考公式:![]() )
)
(3)用线性回归分析的方法,预测小李该月![]() 号打
号打![]() 小时篮球的投篮命中率.
小时篮球的投篮命中率.
查看答案和解析>>
科目: 来源: 题型:
【题目】一台还可以用的机器由于使用的时间较长,它按不同的转速生产出来的某机械零件有一些会有缺陷,每小时生产有缺陷零件的多少随机器运转的速率而变化,下表为抽样试验结果:
转速x(转/秒) | 16 | 14 | 12 | 8 |
每小时生产有缺陷的零件数y(件) | 11 | 9 | 8 | 5 |
(1)画出散点图;
(2)如果y与x有线性相关的关系,求回归直线方程;
(3)若实际生产中,允许每小时生产的产品中有缺陷的零件最多为10个,那么机器的运转速度应控制在什么范围内?
查看答案和解析>>
科目: 来源: 题型:
【题目】设全集U=R,若集合M={y|y= ![]() },N={x|y=lg
},N={x|y=lg ![]() },则(CUM)∩N=( )
},则(CUM)∩N=( )
A.(﹣3,2)
B.(﹣3,0)
C.(﹣∞,1)∪(4,+∞)
D.(﹣3,1)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,![]() ,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G,F分别是EC,BD的中点.
,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G,F分别是EC,BD的中点.

(1)求证:GF∥底面ABC;
(2)求证:AC⊥平面EBC;
(3)求几何体ADEBC的体积V.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
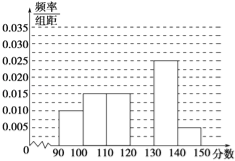
(1)求分数在[120,130)内的频率;
(2)若在同一组数据中,将该组区间的中点值(如:组区间[100,110)的中点值为![]() =105)作为这组数据的平均分,据此,估计本次考试的平均分;
=105)作为这组数据的平均分,据此,估计本次考试的平均分;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线C1在平面直角坐标系中的参数方程为  (t为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,有曲线C2:ρ=2cosθ﹣4sinθ
(t为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,有曲线C2:ρ=2cosθ﹣4sinθ
(1)将C1的方程化为普通方程,并求出C2的平面直角坐标方程
(2)求曲线C1和C2两交点之间的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点
(1)求证:AC 1//平面CDB1;(2)求证:AC⊥面BB1C1C ;

查看答案和解析>>
科目: 来源: 题型:
【题目】设复数z1=(a2-4sin2θ)+(1+2cos θ)i,a∈R,θ∈(0,π),z2在复平面内对应的点在第一象限,且z=-3+4i.
(1)求z2及|z2|.
(2)若z1=z2,求θ与a2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com