
科目: 来源: 题型:
【题目】定义方程f(x)=f′(x)的实数根x0为函数f(x)的“和谐点”.如果函数g(x)=x2(x∈(0,+∞)),h(x)=sin x+2cosx![]() ,φ(x)=ex+x的“和谐点”分别为a,b,c,则a,b,c的大小关系是( )
,φ(x)=ex+x的“和谐点”分别为a,b,c,则a,b,c的大小关系是( )
A. a<b<c B. b<c<a
C. c<b<a D. c<a<b
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=2sin2( ![]() +x)﹣
+x)﹣ ![]() cos2x﹣1,x∈R,若函数k(x)=f(x+a)的图象关于点(﹣
cos2x﹣1,x∈R,若函数k(x)=f(x+a)的图象关于点(﹣ ![]() ,0)对称,且α∈(0,π),则α=( )
,0)对称,且α∈(0,π),则α=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4﹣5:不等式选讲
设函数f(x)=|2x﹣4|+|x+2|
(1)求函数y=f(x)的最小值;
(2)若不等式f(x)≥|a+4|﹣|a﹣3|恒成立,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某大学为调查来自南方和北方的同龄大学生的身高差异,从2016级的年龄在18~19岁之间的大学生中随机抽取了来自南方和北方的大学生各10名,测量他们的身高,量出的身高如下(单位:cm):
南方:158,170,166,169,180,175,171,176,162,163.
北方:183,173,169,163,179,171,157,175,184,166.

(1)根据抽测结果,画出茎叶图,对来自南方和北方的大学生的身高作比较,写出统计结论.
(2)设抽测的10名南方大学生的平均身高为x cm,将10名南方大学生的身高依次输入如图所示的程序框图进行运算,问输出的s大小为多少?并说明s的统计学意义.
(3)为进一步调查身高与生活习惯的关系,现从来自南方的这10名大学生中随机抽取2名身高不低于170 cm的学生,求身高为176 cm的学生被抽中的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线C1的参数方程为 ![]() (其中θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ﹣ρsinθ+1=0.
(其中θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ﹣ρsinθ+1=0.
(1)分别写出曲线C1与曲线C2的普通方程;
(2)若曲线C1与曲线C2交于A,B两点,求线段AB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校高三年级数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,已知成绩在130~140分数段的人数为2.
(1)求这组数据的平均数M.
(2)现根据初赛成绩从第一组和第五组(从低分段至高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成帮扶小组.若选出的两人的成绩之差大于20,则称这两人为“黄金搭档组”,试求选出的两人为“黄金搭档组”的概率.

查看答案和解析>>
科目: 来源: 题型:
【题目】某公司经营一批进价为每件400元的商品,在市场调查时发现,此商品的销售单价x(元)与日销售量y(件)之间的关系如下表所示:
x/元 | 500 | 600 | 700 | 800 | 900 |
y/件 | 10 | 8 | 9 | 6 | 1 |
(1)求y关于x的回归直线方程.
(2)借助回归直线方程,预测销售单价为多少元时,日利润最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=﹣2cosx﹣x+(x+1)ln(x+1),g(x)=k(x2+ ![]() ).其中k≠0.
).其中k≠0.
(1)讨论函数g(x)的单调区间;
(2)若存在x1∈(﹣1,1],对任意x2∈( ![]() ,2],使得f(x1)﹣g(x2)<k﹣6成立,求k的取值范围.
,2],使得f(x1)﹣g(x2)<k﹣6成立,求k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如下:
成绩/m | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 | 1.85 | 1.90 |
人数 | 2 | 3 | 2 | 3 | 4 | 1 | 1 | 1 |
分别求这些运动员的成绩的众数、中位数、平均数(保留到小数点后两位),并分析这些数据的含义.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示的茎叶图记录了甲、乙两组各5名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中用![]() 表示.
表示.
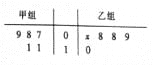
(1)若乙组同学投篮命中次数的平均数比甲组同学的平均数少1,求![]() 及乙组同学投篮命中次数的方差;
及乙组同学投篮命中次数的方差;
(2)在(1)的条件下,分别从甲、乙两组投篮命中次数低于10次的同学中,各随机选取一名,求这两名同学的投篮命中次数之和为16的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com