【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生成绩的中位数是83，乙班学生成绩的平均数是86，则x+y的值为（ ）

A.168
B.169
C.8
D.9

将边长为2的正方形ABCD沿对角线BD折叠，使得平面ABD⊥平面CBD，AE⊥平面ABD，且AE＝．

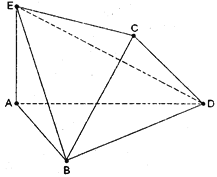
（Ⅰ）求证：DE⊥AC；

（Ⅱ）求DE与平面BEC所成角的正弦值；

（Ⅲ）直线BE上是否存在一点M，使得CM∥平面ADE，若存在，求点M的位置，不存在请说明理由．

【题目】已知抛物线上一点到其焦点的距离为4，椭圆 的离心率，且过抛物线的焦点.

（1）求抛物线和椭圆的标准方程；

（2）过点的直线交抛物线于两不同点，交轴于点，已知， ，求证： 为定值.

【题目】已知函数f（x）= （x＞0）．
（1）试判断函数f（x）在（0，+∞）上单调性并证明你的结论；
（2）若f（x）＞ 恒成立，求整数k的最大值；
（3）求证：（1+1×2）（1+2×3）…[1+n（n+1）]＞e2n﹣3 ．

【题目】抛物线C的方程为y=ax2（a＜0），过抛物线C上一点P（x0 ， y0）（x0≠0）作斜率为k1 ， k2的两条直线分别交抛物线C于A（x1 ， y1）B（x2 ， y2）两点（P，A，B三点互不相同），且满足k2+λk1=0（λ≠0且λ≠﹣1）．
（Ⅰ）求抛物线C的焦点坐标和准线方程；
（Ⅱ）设直线AB上一点M，满足 =λ ，证明线段PM的中点在y轴上；
（Ⅲ）当λ=1时，若点P的坐标为（1，﹣1），求∠PAB为钝角时点A的纵坐标y1的取值范围．

【题目】已知数列{an}的前n项和为Sn ， 且Sn=n2+2n；数列{bn}是公比大于1的等比数列，且满足b1+b4=9，b2b3=8．
（Ⅰ）分别求数列{an}，{bn}的通项公式；
（Ⅱ）若cn=（﹣1）nSn+anbn ， 求数列{cn}的前n项和Tn ．

【题目】如图，四边形ABCD中，AB⊥CD，AD∥BC，AD=3，BC=2AB=2，E，F分别在BC，AD上，EF∥AB．现将四边形ABEF沿EF折起，使平面ABEF⊥平面EFDC．
（Ⅰ）若BE= ，在折叠后的线段AD上是否存在一点P，且 ，使得CP∥平面ABEF？若存在，求出λ的值，若不存在，说明理由；
（Ⅱ）求三棱锥A﹣CDF的体积的最大值，并求此时二面角E﹣AC﹣F的余弦值．

【题目】2016年上半年，股票投资人袁先生同时投资了甲、乙两只股票，其中甲股票赚钱的概率为 ，赔钱的概率是 ；乙股票赚钱的概率为 ，赔钱的概率为 ．对于甲股票，若赚钱则会赚取5万元，若赔钱则损失4万元；对于乙股票，若赚钱则会赚取6万元，若赔钱则损失5万元．
（Ⅰ）求袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率；
（Ⅱ）试求袁先生2016年上半年同事投资甲、乙两只股票的总收益的分布列和数学期望．

【题目】在△ABC中，角A、B、C所对的边分别为a，b，c，cos2C+2 cosC+2=0．
（1）求角C的大小；
（2）若b= a，△ABC的面积为 sinAsinB，求sinA及c的值．

【题目】已知为坐标原点， 是椭圆上的点，设动点满足.

（1）求动点的轨迹的方程；

（2）若直线与曲线相交于， 两个不同点，求面积的最大值.