
科目: 来源: 题型:
【题目】下列结论中,正确的有( )
①不存在实数k,使得方程xlnx﹣ ![]() x2+k=0有两个不等实根;
x2+k=0有两个不等实根;
②已知△ABC中,a,b,c分别为角A,B,C的对边,且a2+b2=2c2 , 则角C的最大值为 ![]() ;
;
③函数y= ![]() ln
ln ![]() 与y=lntan
与y=lntan ![]() 是同一函数;
是同一函数;
④在椭圆 ![]() +
+ ![]() =1(a>b>0),左右顶点分别为A,B,若P为椭圆上任意一点(不同于A,B),则直线PA与直线PB斜率之积为定值.
=1(a>b>0),左右顶点分别为A,B,若P为椭圆上任意一点(不同于A,B),则直线PA与直线PB斜率之积为定值.
A.①④
B.①③
C.①②
D.②④
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=|x﹣a|,若不等式f(x)≤3的解集为{|x|﹣1≤x≤5}. (Ⅰ)求实数a的值:
(Ⅱ)若不等式f(3x)+f(x+3)≥m对一切实数x恒成立,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在直角坐标系xOy中,直线l的参数方程为 ![]() ,若以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρcos2θ+4cosθ=ρ(ρ≥0,0≤θ≤2π).
,若以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρcos2θ+4cosθ=ρ(ρ≥0,0≤θ≤2π).
(Ⅰ)当 ![]() 时,求直线l的普通方程;
时,求直线l的普通方程;
(Ⅱ)若直线l与曲线C相交A,B两点.求证: ![]() 是定值.
是定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=mln(x+1)﹣nx在点(1,f(1))处的切线与y轴垂直,且 ![]() ,其中 m,n∈R.
,其中 m,n∈R.
(Ⅰ)求m,n的值,并求出f(x)的单调区间;
(Ⅱ)设g(x)=﹣x2+2x,确定非负实数a的取值范围,使不等式f(x)+x≥ag(x)在[0,+∞)上恒成立.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线 ![]() 的焦点F1与椭圆
的焦点F1与椭圆 ![]() 的一个焦点重合,Γ的准线与x轴的交点为F1 , 若Γ与C的交点为A,B,且点A到点F1 , F2的距离之和为4.
的一个焦点重合,Γ的准线与x轴的交点为F1 , 若Γ与C的交点为A,B,且点A到点F1 , F2的距离之和为4.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若不过原点且斜率存在的直线l交椭圆C于点G,H,且△OGH的面积为1,线段GH的中点为P.在x轴上是否存在关于原点对称的两个定点M,N,使得直线PM,PN的斜率之积为定值?若存在,求出两定点M,N的坐标和定值的大小;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知矩形ABCD中, ![]() ,点E是边BC上的点,且
,点E是边BC上的点,且 ![]() ,DE与AC相交于点H.现将△ACD沿AC折起,如图2,点D的位置记为D',此时
,DE与AC相交于点H.现将△ACD沿AC折起,如图2,点D的位置记为D',此时 ![]() .
.
(Ⅰ)求证:D'H⊥平面ABC;
(Ⅱ)求二面角H﹣D'E﹣A的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:[20,25),[25,30),[30,35),[35,40),[40,45],并得到如下频率分布直方图.
(Ⅰ)求图中x的值,并根据频率分布直方图统计这600名志愿者中年龄在[30.40)的人数;
(Ⅱ)在抽取的100名志愿者中按年龄分层抽取10名参加区电视台“文明伴你行”节目录制,再从这10名志愿者中随机选取3名到现场分享劝导制止行人闯红灯的经历,记这3名志愿者中年龄不低于35岁的人数为X,求X的分布列及数学期望.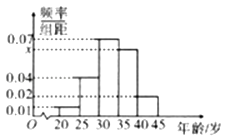
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数 ![]() ,且函数y=f(x)图象的一个对称中心到最近的对称轴的距离为
,且函数y=f(x)图象的一个对称中心到最近的对称轴的距离为 ![]() . (Ⅰ)求ω的值及f(x)的对称柚方程;
. (Ⅰ)求ω的值及f(x)的对称柚方程;
(Ⅱ)在△ABC,中,角A,B,C的对边分別为a,b,c.若 ![]() ,求b的值.
,求b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com