
科目: 来源: 题型:
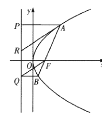
【题目】如图,抛物线![]() 的焦点为
的焦点为![]() ,抛物线
,抛物线![]() 上
上![]() 两点,在抛物线的准线上的射影分别为
两点,在抛物线的准线上的射影分别为![]() .
.
(1)如图,若![]() 点在线段
点在线段![]() 上,过
上,过![]() 作
作![]() 的平行线
的平行线![]() 与抛物线准线交于
与抛物线准线交于![]() ,证明:
,证明:![]() 是
是![]() 的中点;
的中点;
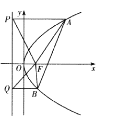
(2)如图,若![]() 的面积是
的面积是![]() 的面积的两倍,求
的面积的两倍,求![]() 中点的轨迹方程.
中点的轨迹方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着智能手机的普及,使用手机上网成为了人们日常生活的一部分,很多消费者对手机流量的需求越来越大.长沙某通信公司为了更好地满足消费者对流量的需求,准备推出一款流量包.该通信公司选了5个城市(总人数、经济发展情况、消费能力等方面比较接近)采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价![]() :(单位:元/月)和购买人数
:(单位:元/月)和购买人数![]() (单位:万人)的关系如表:
(单位:万人)的关系如表:
![]()
(1)根据表中的数据,运用相关系数进行分析说明,是否可以用线性回归模型拟合![]() 与
与![]() 的关系?并指出是正相关还是负相关;
的关系?并指出是正相关还是负相关;
(2)①求出![]() 关于
关于![]() 的回归方程;
的回归方程;
②若该通信公司在一个类似于试点的城市中将这款流量包的价格定位25元/ 月,请用所求回归方程预测长沙市一个月内购买该流量包的人数能否超过20 万人.
参考数据:![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数 ,回归直线方程
,回归直线方程![]() ,
,
其中 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱柱![]() 中,点P,G分别是
中,点P,G分别是![]() ,
,![]() 的中点,已知
的中点,已知![]() ⊥平面ABC,
⊥平面ABC,![]() =
=![]() =3,
=3,![]() =
=![]() =2.
=2.
(I)求异面直线![]() 与AB所成角的余弦值;
与AB所成角的余弦值;
(II)求证:![]() ⊥平面
⊥平面![]() ;
;
(III)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目: 来源: 题型:
【题目】某颜料公司生产A,B两种产品,其中生产每吨A产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨B产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一天之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果A产品的利润为300元/吨,B产品的利润为200元/吨,设公司计划一天内安排生产A产品x吨,B产品y吨.
(I)用x,y列出满足条件的数学关系式,并在下面的坐标系中画出相应的平面区域;
(II)该公司每天需生产A,B产品各多少吨可获得最大利润,最大利润是多少?

查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的是( )
A. 命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
B. 命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
C. “![]() 在
在![]() 处有极值”是“
处有极值”是“![]() ”的充要条件
”的充要条件
D. 命题“若函数![]() 有零点,则“
有零点,则“![]() 或
或![]() ”的逆否命题为真命题
”的逆否命题为真命题
查看答案和解析>>
科目: 来源: 题型:
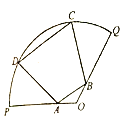
【题目】为丰富市民的文化生活,市政府计划在一块半径为200m,圆心角为![]() 的扇形地上建造市民广场,规划设计如图:内接梯形
的扇形地上建造市民广场,规划设计如图:内接梯形![]() 区域为运动休闲区,其中A,B分别在半径
区域为运动休闲区,其中A,B分别在半径![]() ,
,![]() 上,C,D在圆弧
上,C,D在圆弧![]() 上,
上,
![]() ;上,
;上,![]() ;
;![]() 区域为文化展区,
区域为文化展区,![]() 长为
长为![]() ,其余空地为绿化区域,且
,其余空地为绿化区域,且![]() 长不得超过200m.
长不得超过200m.
(1)试确定A,B的位置,使![]() 的周长最大?
的周长最大?
(2)当![]() 的周长最长时,设
的周长最长时,设![]() ,试将运动休闲区
,试将运动休闲区![]() 的面积S表示为
的面积S表示为![]() 的函数,并求出S的最大值.
的函数,并求出S的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂生产某种型号的电视机零配件,为了预测今年![]() 月份该型号电视机零配件的市场需求量,以合理安排生产,工厂对本年度
月份该型号电视机零配件的市场需求量,以合理安排生产,工厂对本年度![]() 月份至
月份至![]() 月份该型号电视机零配件的销售量及销售单价进行了调查,销售单价
月份该型号电视机零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的
(单位:千件)之间的![]() 组数据如下表所示:
组数据如下表所示:
月份 |
|
|
|
|
|
|
销售单价 |
|
|
|
|
|
|
销售量 |
|
|
|
|
|
|
(1)根据1至![]() 月份的数据,求
月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() );
);
(2)结合(1)中的线性回归方程,假设该型号电视机零配件的生产成本为每件![]() 元,那么工厂如何制定
元,那么工厂如何制定![]() 月份的销售单价,才能使该月利润达到最大(计算结果精确到
月份的销售单价,才能使该月利润达到最大(计算结果精确到![]() )?
)?
参考公式:回归直线方程![]() ,其中
,其中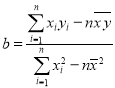 .
.
参考数据:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,且满足
上,且满足![]() ,(
,(![]() 为坐标原点).
为坐标原点).
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 作斜率乘积为1的两条不重合的直线
作斜率乘积为1的两条不重合的直线![]() ,且
,且![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点分别为
的中点分别为![]() ,求证:直线
,求证:直线![]() 过定点,并求出定点坐标.
过定点,并求出定点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com