
科目: 来源: 题型:
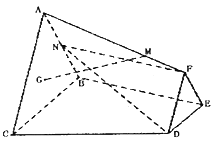
【题目】如图,已知![]() 与
与![]() 分别是边长为1与2的正三角形,
分别是边长为1与2的正三角形,![]() ,四边形
,四边形![]() 为直角梯形,且
为直角梯形,且![]() ,
,![]() ,点
,点![]() 为
为![]() 的重心,
的重心,![]() 为
为![]() 中点,
中点,![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 上靠近点
上靠近点![]() 的三等分点.
的三等分点.
(1)求证:![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值为
的余弦值为![]() ,试求异面直线
,试求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某食品集团生产的火腿按行业生产标准分成8个等级,等级系数![]() 依次为1,2,3,…,8,其中
依次为1,2,3,…,8,其中![]() 为标准
为标准![]() ,
, ![]() 为标准
为标准![]() .已知甲车间执行标准
.已知甲车间执行标准![]() ,乙车间执行标准
,乙车间执行标准![]() 生产该产品,且两个车间的产品都符合相应的执行标准.
生产该产品,且两个车间的产品都符合相应的执行标准.
(1)已知甲车间的等级系数![]() 的概率分布列如下表,若
的概率分布列如下表,若![]() 的数学期望E(X1)=6.4,求
的数学期望E(X1)=6.4,求![]() ,
, ![]() 的值;
的值;
X1 | 5 | 6 | 7 | 8 |
P | 0.2 |
|
|
|
(2)为了分析乙车间的等级系数![]() ,从该车间生产的火腿中随机抽取30根,相应的等级系数组成一个样本如下:3 5 3 3 8 5 5 6 3 4 6 3 4 7 5 3 4 8 5 3 8 3 4 3 4 4 7 5 6 7
,从该车间生产的火腿中随机抽取30根,相应的等级系数组成一个样本如下:3 5 3 3 8 5 5 6 3 4 6 3 4 7 5 3 4 8 5 3 8 3 4 3 4 4 7 5 6 7
用该样本的频率分布估计总体,将频率视为概率,求等级系数![]() 的概率分布列和均值;
的概率分布列和均值;
(3)从乙车间中随机抽取5根火腿,利用(2)的结果推断恰好有三根火腿能达到标准![]() 的概率.
的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小明的父母至少有一人与他相邻,则不同坐法的总数为
A. 60 B. 72 C. 84 D. 96
查看答案和解析>>
科目: 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对家庭用水情况进行了调查,通过抽样,获得了某年100个家庭的月均用水量(单位:t),将数据按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成5组,制成了如图所示的频率分布直方图.
分成5组,制成了如图所示的频率分布直方图.
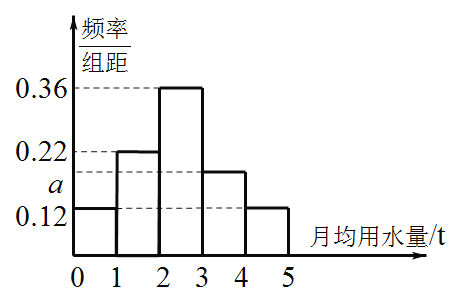
(1)求图中a的值;
(2)设该市有10万个家庭,估计全市月均用水量不低于![]() 的家庭数;
的家庭数;
(3)假设同组中的每个数据都用该组区间的中点值代替,估计全市家庭月均用水量的平均数.
查看答案和解析>>
科目: 来源: 题型:
【题目】有120粒试验种子需要播种,现有两种方案:方案一:将120粒种子分种在40个坑内,每坑3粒;方案二:120粒种子分种在60个坑内,每坑2粒 如果每粒种子发芽的概率为0.5,并且,若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种(每个坑至多补种一次,且第二次补种的种子颗粒同第一次).假定每个坑第一次播种需要2元,补种1个坑需1元;每个成活的坑可收货100粒试验种子,每粒试验种子收益1元.
(1)用![]() 表示播种费用,分别求出两种方案的
表示播种费用,分别求出两种方案的![]() 的数学期望;
的数学期望;
(2)用![]() 表示收益,分别求出两种方案的收益
表示收益,分别求出两种方案的收益![]() 的数学期望;
的数学期望;
(3)如果在某块试验田对该种子进行试验,你认为应该选择哪种方案?
查看答案和解析>>
科目: 来源: 题型:
【题目】甲乙两人同时生产内径为![]() 的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各抽出 5 件(单位:
的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各抽出 5 件(单位: ![]() ) ,
) ,
甲:25.44,25.43, 25.41,25.39,25.38
乙:25.41,25.42, 25.41,25.39,25.42.
从生产的零件内径的尺寸看、谁生产的零件质量较高.
查看答案和解析>>
科目: 来源: 题型:
【题目】空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的质量指数.空气质量按照AQI大小分为六级:0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.一环保人士记录去年某地某月10天的AQI的茎叶图如图.利用该样本估计该地本月空气质量优良(![]() )的天数(按这个月总共30天计算)为________.
)的天数(按这个月总共30天计算)为________.

查看答案和解析>>
科目: 来源: 题型:
【题目】某校高一年级开设了丰富多彩的校本课程,现从甲、乙两个班随机抽取了5名学生校本课程的学分,统计如下表.
甲 | 8 | 11 | 14 | 15 | 22 |
乙 | 6 | 7 | 10 | 23 | 24 |
用![]() 分别表示甲、乙两班抽取的5名学生学分的方差,计算两个班学分的方差.得
分别表示甲、乙两班抽取的5名学生学分的方差,计算两个班学分的方差.得![]() ______,并由此可判断成绩更稳定的班级是______班.
______,并由此可判断成绩更稳定的班级是______班.
查看答案和解析>>
科目: 来源: 题型:
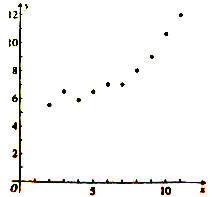
【题目】某公司近年来特别注重创新产品的研发,为了研究年研发经费![]() (单位:万元)对年创新产品销售额
(单位:万元)对年创新产品销售额![]() (单位:十万元)的影响,对近10年的研发经费
(单位:十万元)的影响,对近10年的研发经费![]() 与年创新产品销售额
与年创新产品销售额![]() (
(![]() ,10)的数据作了初步处理,得到如图的散点图及一些统计量的值.
,10)的数据作了初步处理,得到如图的散点图及一些统计量的值.
其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
现拟定![]() 关于
关于![]() 的回归方程为
的回归方程为![]() .
.
(1)求![]() ,
,![]() 的值(结果精确到0.1);
的值(结果精确到0.1);
(2)根据拟定的回归方程,预测当研发经费为13万元时,年创新产品销售额是多少?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为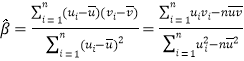 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com