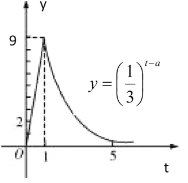
(Ⅰ)写出服药一次后y与t之间的函数关系式；

(Ⅱ)据进一步测定：每毫升血液中含药量不少于微克时，治疗有效，求服药一次后治疗有效的时间是多长？

【题目】（1）已知函数，其中，求函数的图象恰好经过第一、二、三象限的概率；

（2）某校早上8:10开始上课，假设该校学生小张与小王在早上7:30～8:00之间到校，且每人到该时间段内到校时刻是等可能的，求两人到校时刻相差10分钟以上的概率.

①抛物线的准线方程为；

②过点作与抛物线只有一个公共点的直线仅有1条；

③是抛物线上一动点，以为圆心作与抛物线准线相切的圆，则此圆一定过定点.

④抛物线上到直线距离最短的点的坐标为.

【题目】2018年秋季，我省高一年级全面实行新高考政策，为了调查学生对新政策的了解情况，准备从某校高一三个班级抽取10名学生参加调查.已知三个班级学生人数分别为40人，30人，30人.考虑使用简单随机抽样、分层抽样和系统抽样三种方案，使用简单随机抽样和分层抽样时，将学生按三个班级依次统一编号为1,2，…，100；使用系统抽样，将学生统一编号为1,2，…，100，并将整个编号依次分为10段.如果抽得的号码有下列四种情况：

①7,17,27,37,47,57,67,77，87,97；②3,9,15,33,43,53,65,75,85,95；

③9,19,29,39,49,59,69,79,89,99,；④2,12,22,32,42,52,62,73,83,96.

关于上述样本的下列结论中，正确的是（ ）

A. ①③都可能为分层抽样 B. ②④都不能为分层抽样

C. ①④都可能为系统抽样 D. ②③都不能为系统抽样

【题目】某调查机构对本市小学生课业负担情况进行了调查，设平均每人每天做作业的时间为分钟，有1200名小学生参加了此项调查，调查所得到的数据用程序框图处理（如图），若输出的结果是840，若用样本频率估计概率，则平均每天做作业的时间在0～60分钟内的学生的概率是（ ）

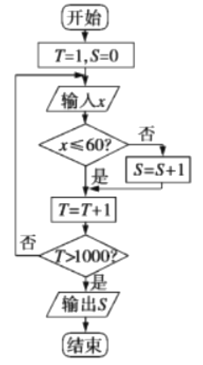
A. 0.32 B. 0.36 C. 0.7 D. 0.84

【题目】如图，在四棱锥中， ， ， 两两垂直， ，且， .

（1）求二面角的余弦值；

（2）已知点为线段上异于的点，且，求的值.

【题目】（1）已知函数，其中，求函数的图象恰好经过第一、二、三象限的概率；

（2）某校早上8:10开始上课，假设该校学生小张与小王在早上7:30～8:00之间到校，且每人到该时间段内到校时刻是等可能的，求两人到校时刻相差10分钟以上的概率.

(1)求函数f(x)的解析式；

(2)若－1＜f(1)＜1，求实数a的取值范围．

【题目】若数列同时满足：①对于任意的正整数， 恒成立；②对于给定的正整数， 对于任意的正整数恒成立，则称数列是“数列”.

（1）已知判断数列是否为“数列”，并说明理由；

（2）已知数列是“数列”，且存在整数，使得， ， ， 成等差数列，证明： 是等差数列.

【题目】为了了解我市参加2018年全国高中数学联赛的学生考试结果情况，从中选取60名同学将其成绩（百分制，均为正数）分成六组后，得到部分频率分布直方图（如图），观察图形，回答下列问题：

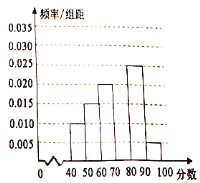
（1）求分数在内的频率，并补全这个频率分布直方图；

（2）根据频率分布直方图，估计本次考试成绩的众数、中位数、均值.