【题目】给出函数如下表，则f〔g（x）〕的值域为（ ）

A. {4,2} B. {1,3} C. {1,2,3,4} D. 以上情况都有可能

【题目】已知函数．

（1）若函数y＝f(x)为偶函数，求k 的值；

（2）求函数y＝f(x)在区间[0，4]上的最大值；

（3）若方程f(x)=0 有且仅有一个根，求实数k 的取值范围．

【题目】为了解华师一附中学生喜欢吃辣是否与性别有关，调研部(共10人)分三组对高中三个年级的学生进行调查，每个年级至少派3个人进行调查.(1)求调研部的甲、乙两人都被派到高一年级进行调查的概率.(2)调研部对三个年级共100人进行了调查，得到如下的列联表，请将列联表补充完整，并判断是否有以上的把握认为喜欢吃辣与性别有关？

参考数据：

参考公式：，其中.

【题目】已知是定义在R上的偶函数,当时, .

（1）求的解析式；并画出简图；

（2）利用图象讨论方程的根的情况。(只需写出结果,不要解答过程)．

（3）若直线与函数的图像自左向右依次交于四个不同点 A,B,C,D .若AB=BC，求实数k的值.

【题目】如图，在正方体中，，分别是棱，的中点，为棱上一点，且平面.

（1）证明：为中点；

（2）求平面与平面所成锐二面角的余弦值.

【题目】某农业合作社生产了一种绿色蔬菜共吨，如果在市场上直接销售，每吨可获利万元；如果进行精加工后销售，每吨可获利万元，但需另外支付一定的加工费，总的加工（万元）与精加工的蔬菜量（吨）有如下关系：设该农业合作社将（吨）蔬菜进行精加工后销售，其余在市场上直接销售，所得总利润（扣除加工费）为（万元）．

（1）写出关于的函数表达式；

（2）当精加工蔬菜多少吨时，总利润最大，并求出最大利润．

【题目】某家电公司根据销售区域将销售员分成，两组.年年初，公司根据销售员的销售业绩分发年终奖，销售员的销售额（单位：十万元）在区间，，，内对应的年终奖分别为2万元，2.5万元，3万元，3.5万元.已知销售员的年销售额都在区间内，将这些数据分成4组：，，，，得到如下两个频率分布直方图：

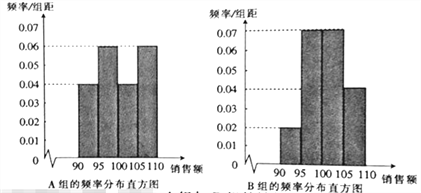
以上面数据的频率作为概率，分别从组与组的销售员中随机选取1位，记，分别表示组与组被选取的销售员获得的年终奖.

（1）求的分布列及数学期望；

（2）试问组与组哪个组销售员获得的年终奖的平均值更高？为什么？

(1)某学校从编号依次为001，002，…，900的900个学生中用系统抽样的方法抽取一个样本，已知样本中有两个相邻的编号分别为053，098，则样本中最大的编号为862.

(2)甲组数据的方差为5，乙组数据为5、6、9、10、5，那么这两组数据中较稳定的是甲.

(3)若两个变量的线性相关性越强，则相关系数的值越接近于1.

(4)对A、B、C三种个体按3:1:2的比例进行分层抽样调查，若抽取的A种个体有15个，则样本容量为30.

则正确的个数是

A. 3 B. 2 C. 1 D. 0

【题目】已知定义在R上的函数满足:①对于任意的都有成立;②当时,;③;则不等式的解集为__________.

【题目】设是等差数列，是各项都为正数的等比数列，且，.

（1）求,的通项公式；

（2）设，，若，，成等差数列（、为正整数且），求和的值；

（3）设为数列的前项和，是否存在实数，使得对一切均成立？若存在，求出的最大值；若不存在，说明理由.