A. 10000立方尺 B. 11000立方尺

C. 12000立方尺 D. 13000立方尺

【题目】阿波罗尼斯是古希腊著名数学家，与欧几里得、阿基米德被称为亚历山大时期数学三巨匠，他对圆锥曲线有深刻而系统的研究，主要研究成果集中在他的代表作《圆锥曲线》一书，阿波罗尼斯圆是他的研究成果之一，指的是：已知动点M与两定点A、B的距离之比为λ（λ＞0，λ≠1），那么点M的轨迹就是阿波罗尼斯圆．下面，我们来研究与此相关的一个问题．已知圆：x2+y2＝1和点，点B（1，1），M为圆O上动点，则2|MA|+|MB|的最小值为_____．

①三棱锥D1﹣B1EF的体积为定值；

②异面直线D1B1与EF所成的角为45°；

③D1B1⊥平面B1EF；

④直线D1B1与平面B1EF所成的角为60°．

其中正确的命题为_____．

【题目】函数.

（1）若，试讨论函数的单调性；

（2）若有两个零点，求的取值范围.

【题目】已知椭圆C：+=1（a＞b＞0）的离心率为，直线l：x+2y=4与椭圆有且只有一个交点T．

（I）求椭圆C的方程和点T的坐标；

（Ⅱ）O为坐标原点，与OT平行的直线l′与椭圆C交于不同的两点A，B，直线l′与直线l交于点P，试判断是否为定值，若是请求出定值，若不是请说明理由．

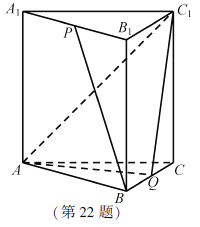
（1）求异面直线BP与AC1所成角的余弦值；

（2）求直线CC1与平面AQC1所成角的正弦值．

【题目】为净化新安江水域的水质，市环保局于2017年底在新安江水域投入一些蒲草，这些蒲草在水中的蔓延速度越来越快，2018年二月底测得蒲草覆盖面积为，2018年三月底测得覆盖面积为，蒲草覆盖面积（单位：）与月份（单位：月）的关系有两个函数模型与可供选择.

（Ⅰ）分别求出两个函数模型的解析式；

（Ⅱ）若市环保局在2017年年底投放了的蒲草，试判断哪个函数模型更合适？并说明理由；

（Ⅲ）利用（Ⅱ）的结论，求蒲草覆盖面积达到的最小月份．

（参考数据：，）

【题目】已知函数对任意实数x、y恒有，当x>0时，f(x)<0，且.

(1)判断的奇偶性；

(2)求在区间[-3,3]上的最大值；

(3)若对所有的恒成立，求实数的取值范围.

【题目】已知抛物线：，圆：，直线：与抛物线相切于点，与圆相切于点.

（1）若直线的斜率，求直线和抛物线的方程；

（2）设为抛物线的焦点，设，的面积分别为，，若，求的取值范围.