
科目: 来源: 题型:
【题目】如图,在四棱锥PABCD中,AB∥CD ,且∠BAP=∠CDP =90°.

(1).证明:平面PAB⊥平面PAD;
(2).若PA=PD=AB=DC, ∠APD =90°,且四棱锥PABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的右顶点、上顶点分别为
的右顶点、上顶点分别为![]() 、
、![]() ,坐标原点到直线
,坐标原点到直线![]() 的距离为
的距离为![]() ,且
,且![]() ,则椭圆
,则椭圆![]() 的方程为( )
的方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
写出直线![]() 的方程,利用原点到直线
的方程,利用原点到直线![]() 的距离,以及
的距离,以及![]() 列方程组,解方程组求得
列方程组,解方程组求得![]() 的值,进而求得椭圆的方程.
的值,进而求得椭圆的方程.
椭圆右顶点坐标为![]() ,上顶点坐标为
,上顶点坐标为![]() ,故直线
,故直线![]() 的方程为
的方程为![]() ,即
,即![]() ,依题意原点到直线的距离为
,依题意原点到直线的距离为![]() ,且
,且![]() ,由此解得
,由此解得![]() ,故椭圆的方程为
,故椭圆的方程为![]() ,故选D.
,故选D.
【点睛】
本小题主要考查过两点的直线方程,考查点到直线的距离公式,考查椭圆标准方程的求法,考查了方程的思想.属于中档题.
【题型】单选题
【结束】
11
【题目】若实数![]() ,
,![]() 满足
满足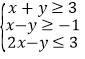 ,则
,则![]() 的最小值是( )
的最小值是( )
A. 0 B. ![]() C. -6 D. -3
C. -6 D. -3
查看答案和解析>>
科目: 来源: 题型:
【题目】下列命题:
①若![]() 是定义在
是定义在![]() 上的偶函数,且在
上的偶函数,且在![]() 上是增函数,
上是增函数,![]() ,则
,则![]() ;
;
②若锐角![]() 、
、![]() 满足c
满足c![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() 对
对![]() 恒成立;
恒成立;
④要得到![]() 的图像,只需将
的图像,只需将![]() 的图像向右平移
的图像向右平移![]() 个单位:
个单位:
其中真命题的个数有( )
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】某商品近一个月内(30天)预计日销量![]() (件)与时间t(天)的关系如图1所示,单价
(件)与时间t(天)的关系如图1所示,单价![]() (万元/件)与时间t(天)的函数关系如图2所示,(t为整数)
(万元/件)与时间t(天)的函数关系如图2所示,(t为整数)
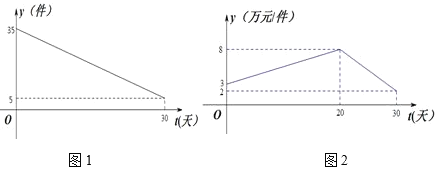
(1)试写出![]() 与
与![]() 的解析式;
的解析式;
(2)求此商品日销售额的最大值?
查看答案和解析>>
科目: 来源: 题型:
【题目】过抛物线![]() 的焦点作直线交抛物线于
的焦点作直线交抛物线于![]() ,
,![]() 两点,若
两点,若![]() ,则
,则![]() 的值为( )
的值为( )
A. 10 B. 8 C. 6 D. 4
【答案】B
【解析】
根据过抛物线焦点的弦长公式,利用题目所给已知条件,求得弦长![]() .
.
根据过抛物线焦点的弦长公式有![]() .故选B.
.故选B.
【点睛】
本小题主要考查过抛物线焦点的弦长公式,即![]() .要注意只有过抛物线焦点的弦长才可以使用.属于基础题.
.要注意只有过抛物线焦点的弦长才可以使用.属于基础题.
【题型】单选题
【结束】
10
【题目】已知椭圆![]() :
: ![]() 的右顶点、上顶点分别为
的右顶点、上顶点分别为![]() 、
、![]() ,坐标原点到直线
,坐标原点到直线![]() 的距离为
的距离为![]() ,且
,且![]() ,则椭圆
,则椭圆![]() 的方程为( )
的方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ADC=60°,侧面PDC是正三角形,平面PDC⊥平面ABCD,CD=2,M为PB的中点.

(1)求证:PA⊥平面CDM.
(2)求二面角D-MC-B的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=![]() ,∠BAD=120°.
,∠BAD=120°.
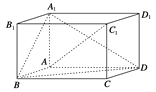
(1)求异面直线A1B与AC1所成角的余弦值;
(2)求二面角B-A1D-A的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市每年春节前后,由于大量的烟花炮竹的燃放,空气污染较为严重.该市环保研究所对近年春节前后每天的空气污染情况调查研究后发现,每天空气污染的指数.f(t),随时刻t(时)变化的规律满足表达式![]() ,其中a为空气治理调节参数,且a∈(0,1).
,其中a为空气治理调节参数,且a∈(0,1).
(1)令![]() ,求x的取值范围;
,求x的取值范围;
(2)若规定每天中f(t)的最大值作为当天的空气污染指数,要使该市每天的空气污染指数不超过5,试求调节参数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com