
科目: 来源: 题型:
【题目】设f(n)是定义在N*上的增函数,f(4)=5,且满足:
①任意n∈N*,f(n)![]() Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
(1)求f(1),f(2),f(3)的值;
(2)求f(n)的表达式.
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年春节突如其来的新型冠状病毒肺炎在湖北爆发,为了打赢疫情防控阻击战,我们执行了延长假期政策,在延长假期面前,我们“停课不停学”,河南省教育厅组织部分优秀学校的优秀教师录播《名师同步课堂》,我校高一年级要在甲、乙、丙、丁、戊5位数学教师中随机抽取3人参加录播课堂,则甲、乙两位教师同时被选中的概率为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
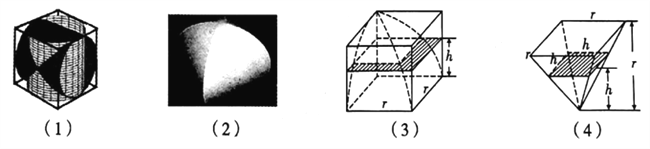
【题目】中国古代数学家刘徽在《九章算术注》中,称一个正方体内两个互相垂直的内切圆柱所围成的立体为“牟合方盖”,如图(1)(2),刘徽未能求得牟合方盖的体积,直言“欲陋形措意,惧失正理”,不得不说“敢不阙疑,以俟能言者”.约200年后,祖冲之的儿子祖暅提出“幂势既同,则积不容异”,后世称为祖暅原理,即:两等高立体,若在每一等高处的截面积都相等,则两立体体积相等.如图(3)(4),祖暅利用八分之一正方体去掉八分之一牟合方盖后的几何体与长宽高皆为八分之一正方体的边长的倒四棱锥“等幂等积”,计算出牟合方盖的体积,据此可知,牟合方盖的体积与其外切正方体的体积之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙、丙、丁四位同学参加比赛,只有其中三位获奖.甲说:“乙或丙未获奖”;乙说:“甲、丙都获奖”;丙说:“我未获奖”;丁说:“乙获奖”.四位同学的话恰有两句是对的,则( )
A. 甲和乙不可能同时获奖 B. 丙和丁不可能同时获奖
C. 乙和丁不可能同时获奖 D. 丁和甲不可能同时获奖
【答案】C
【解析】若甲乙丙同时获奖,则甲丙的话错,乙丁的话对;符合题意;
若甲乙丁同时获奖,则乙的话错,甲丙丁的话对;不合题意;
若甲丙丁同时获奖,则丙丁的话错,甲乙的话对;符合题意;;
若丙乙丁同时获奖,则甲乙丙的话错,丁的话对;不合题意;
因此乙和丁不可能同时获奖,选C.
【题型】单选题
【结束】
12
【题目】已知当![]() 时,关于
时,关于![]() 的方程
的方程![]() 有唯一实数解,则
有唯一实数解,则![]() 值所在的范围是( )
值所在的范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() :
:![]() ,半径为2的圆
,半径为2的圆![]() 与
与![]() 相切,圆心
相切,圆心![]() 在
在![]() 轴上且在直线
轴上且在直线![]() 的右上方.
的右上方.
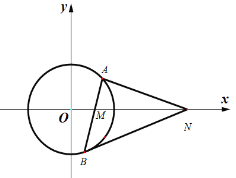
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 的直线与圆
的直线与圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 轴上方),问在
轴上方),问在![]() 轴正半轴上是否存在定点
轴正半轴上是否存在定点![]() ,使得
,使得![]() 轴平分
轴平分![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知等比数列![]() 的公比
的公比![]() ,前
,前![]() 项和为
项和为![]() ,且满足
,且满足![]() .
.![]() ,
,![]() ,
,![]() 分别是一个等差数列的第1项,第2项,第5项.
分别是一个等差数列的第1项,第2项,第5项.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若![]() ,
,![]() 的前
的前![]() 项和为
项和为![]() ,且对任意的
,且对任意的![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】设![]() 是两条不同的直线,
是两条不同的直线, ![]() 是两个不同的平面,则下列命题中正确的是( )
是两个不同的平面,则下列命题中正确的是( )
A. 若![]() ,
, ![]() ,则
,则![]()
B. 若![]() ,
, ![]() ,则
,则![]()
C. 若![]() ,
, ![]() ,
, ![]() ,则
,则![]()
D. 若![]() ,且
,且![]() ,点
,点![]() ,直线
,直线![]() ,则
,则![]()
【答案】C
【解析】A. 若![]() ,
, ![]() ,则
,则![]() 或
或![]() ;
;
B. 若![]() ,
, ![]() ,则
,则![]() 无交点,即平行或异面;
无交点,即平行或异面;
C. 若![]() ,
, ![]() ,
, ![]() ,过
,过![]() 作平面与
作平面与![]() 分别交于直线s,t,则
分别交于直线s,t,则![]() ,
, ![]() ,所以
,所以![]() t,再根据线面平行判定定理得
t,再根据线面平行判定定理得![]() ,因为
,因为![]() ,
, ![]() ,所以
,所以![]() ,即
,即![]()
D. 若![]() ,且
,且![]() ,点
,点![]() ,直线
,直线![]() ,当B在平面
,当B在平面![]() 内时才有
内时才有![]() ,
,
综上选C.
【题型】单选题
【结束】
11
【题目】甲、乙、丙、丁四位同学参加比赛,只有其中三位获奖.甲说:“乙或丙未获奖”;乙说:“甲、丙都获奖”;丙说:“我未获奖”;丁说:“乙获奖”.四位同学的话恰有两句是对的,则( )
A. 甲和乙不可能同时获奖 B. 丙和丁不可能同时获奖
C. 乙和丁不可能同时获奖 D. 丁和甲不可能同时获奖
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com