
科目: 来源: 题型:
【题目】已知数列{an}满足a1=![]() ,an+1=3an-1(n∈N*).
,an+1=3an-1(n∈N*).
(1)若数列{bn}满足bn=an-![]() ,求证:{bn}是等比数列;
,求证:{bn}是等比数列;
(2)求数列{an}的前n项和Sn.
查看答案和解析>>
科目: 来源: 题型:
【题目】意大利著名数学家斐波那契在研究兔子的繁殖问题时,发现有这样的一列数:1,1,2,3,5,8,…,该数列的特点是:前两个数均为1,从第三个数起,每一个数都等于它前面两个数的和.人们把这样的一列数组成的数列![]() 称为斐波那契数列. 并将数列
称为斐波那契数列. 并将数列![]() 中的各项除以4所得余数按原顺序构成的数列记为
中的各项除以4所得余数按原顺序构成的数列记为![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知三棱锥![]() 的三条侧棱
的三条侧棱![]() ,
, ![]() ,
, ![]() 两两垂直,
两两垂直, ![]() 为等边三角形,
为等边三角形, ![]() 为
为![]() 内部一点,点
内部一点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
(Ⅰ)证明: ![]() ;
;
(Ⅱ)证明: ![]() ;
;
(Ⅲ)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥P—ABCD的底面是边长为a的棱形,PD⊥底面ABCD.

(1)证明:AC⊥平面PBD;
(2)若PD=AD,直线PB与平面ABCD所成的角为45°,四棱锥P—ABCD的体积为![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
查看答案和解析>>
科目: 来源: 题型:
【题目】“冰桶挑战赛”是一项社交网络上发起的慈善公益活动,活动规定:被邀请者要么在![]() 小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外
小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外![]() 个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
(1)若某参与者接受挑战后,对其他![]() 个人发出邀请,则这
个人发出邀请,则这![]() 个人中至少有
个人中至少有![]() 个人接受挑战的概率是多少?
个人接受挑战的概率是多少?
(2)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构进行了随机抽样调查,调查得到如下列联表:
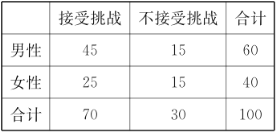
根据表中数据,能否有![]() %的把握认为“冰桶挑战赛与受邀者的性别有关”?
%的把握认为“冰桶挑战赛与受邀者的性别有关”?
附: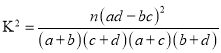

查看答案和解析>>
科目: 来源: 题型:
【题目】在标有“甲”的袋中有![]() 个红球和
个红球和![]() 个白球,这些球除颜色外完全相同.
个白球,这些球除颜色外完全相同.
(Ⅰ)若从袋中依次取出![]() 个球,求在第一次取到红球的条件下,后两次均取到白球的概率;
个球,求在第一次取到红球的条件下,后两次均取到白球的概率;
(Ⅱ)现从甲袋中取出个![]() 红球,
红球, ![]() 个白球,装入标有“乙”的空袋.若从甲袋中任取
个白球,装入标有“乙”的空袋.若从甲袋中任取![]() 球,乙袋中任取
球,乙袋中任取![]() 球,记取出的红球的个数为
球,记取出的红球的个数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,函数
,函数![]() (
(![]() 是自然对数的底数).
是自然对数的底数).
(Ⅰ)若![]() ,证明:曲线
,证明:曲线![]() 没有经过点
没有经过点![]() 的切线;
的切线;
(Ⅱ)若函数![]() 在其定义域上不单调,求
在其定义域上不单调,求![]() 的取值范围;
的取值范围;
(Ⅲ)是否存在正整数![]() ,当
,当![]() 时,函数
时,函数![]() 的图象在
的图象在![]() 轴的上方,若存在,求
轴的上方,若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com