【题目】为选拔选手参加“中国诗词大会”，某中学举行一次“诗词大赛”活动.为了了解本次竞赛学生的成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为）进行统计.按照， ， ， ， 的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在， 的数据）.

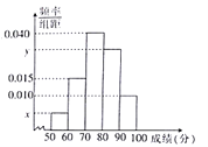
（1）求样本容量和频率分布直方图中、的值；

（2）在选取的样本中，从竞赛成绩在80分以上（含80分）的学生中随机抽取2名学生参加“中国谜语大会”，设随机变量表示所抽取的2名学生中得分在内的学生人数，求随机变量的分布列及数学期望.

① 向左平移个单位长度，再将每个点的横坐标缩短为原来的;

② 向右平移个单位长度，再将每个点的横坐标缩短为原来的;

③ 每个点的横坐标缩短为原来的，向右平移个单位长度;

④ 每个点的横坐标缩短为原来的，向左平移个单位长度;

其中能将的图像变换成函数的图像的是（ ）

A.①和③ B.①和④ C.②和④ D.②和③

如图，四边形ABCD为正方形，QA⊥平面ABCD，PD∥QA，QA=AB=PD．

（I）证明：PQ⊥平面DCQ；

（II）求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值．

【题目】已知函数 (是自然对数的底数)， .

（1）求曲线在点处的切线方程；

（2）求的单调区间；

（3）设，其中为的导函数，证明：对任意.

【题目】图一是美丽的“勾股树”，它是一个直角三角形分别以它的每一边向外作正方形而得到．图二是第1代“勾股树”，重复图二的作法，得到图三为第2代“勾股树”，以此类推，已知最大的正方形面积为1，则第代“勾股树”所有正方形的个数与面积的和分别为（ ）

A. B. C. D.

【题目】如图是函数的导函数的图象，给出下列命题：

①-2是函数的极值点；

②1是函数的极值点；

③的图象在处切线的斜率小于零；

④函数在区间上单调递增.

则正确命题的序号是（ ）

A. ①③ B. ②④ C. ②③ D. ①④

已知函数.

（Ⅰ）解不等式： ；

（Ⅱ）当时，函数的图象与轴围成一个三角形，求实数的取值范围.

【题目】已知函数，其中.

（1）讨论的单调性；

（2）当时，证明:；

（3）求证：对任意的，都有：，(其中为自然对数的底数)。

（1）根据以上列联表，问能否在犯错误的概率不超过0.05的前提下认为观众性别与喜爱该演讲有关．（精确到0．001）

（2）从这60名男观众中按对该演讲是否喜爱采取分层抽样，抽取一个容量为6的样本，然后随机选取两名作跟踪调查，求选到的两名观众都喜爱该演讲的概率．

附：临界值表

参考公式：，．

【题目】已知函数 有两个不同的零点.

（1）求的取值范围；

（2）设， 是的两个零点，证明： .