
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,已知直线l:![]() -y+3+
-y+3+![]() =0和圆
=0和圆![]() :
:![]() +
+![]() +8x+F=0.若直线l被圆
+8x+F=0.若直线l被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)设圆![]() 和x轴相交于A,B两点,点P为圆
和x轴相交于A,B两点,点P为圆![]() 上不同于A,B的任意一点,直线PA,PB交y轴于M,N两点.当点P变化时,以MN为直径的圆
上不同于A,B的任意一点,直线PA,PB交y轴于M,N两点.当点P变化时,以MN为直径的圆![]() 是否经过圆
是否经过圆![]() 内一定点?请证明你的结论;
内一定点?请证明你的结论;
(3)若△RST的顶点R在直线x=-1上,点S,T在圆![]() 上,且直线RS过圆心
上,且直线RS过圆心![]() ,∠SRT=
,∠SRT=![]() ,求点R的纵坐标的范围.
,求点R的纵坐标的范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
(Ⅰ)根据以上资料完成下面的2×2列联表,若据此数据算得![]() ,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?
,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?

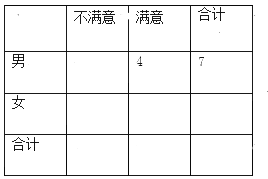
附:

(Ⅱ) 估计用户对该公司的产品“满意”的概率;
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着互联网的快速发展,基于互联网的共享单车应运而生,某市场研究人员为了了解共享单车运营公司![]() 的经营状况,对该公司最近六个月的市场占有率进行了统计,并绘制了相应的折线图:
的经营状况,对该公司最近六个月的市场占有率进行了统计,并绘制了相应的折线图:
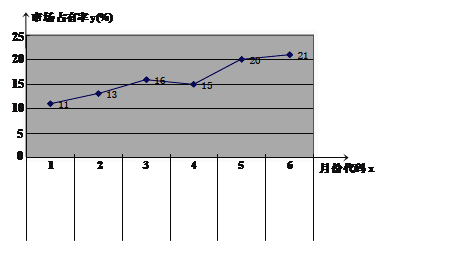
(1)由折线图可以看出,可用线性回归模型拟合月度市场占有率![]() 与月份代码
与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并
的线性回归方程,并
预测![]() 公司2017年4月的市场占有率;
公司2017年4月的市场占有率;
(2)为进一步扩大市场,公司拟再采购一批单车,现有采购成本分别为![]() 元/辆和1200元/辆的
元/辆和1200元/辆的![]() 、
、![]() 两款车型可供选择,按规定每辆单车最
两款车型可供选择,按规定每辆单车最
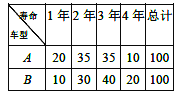
多使用4年,但由于多种原因(如骑行频率等)会导致单车使用寿命各不相同,考虑到公司运营的经济效益,该公司决定先对这两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命的频数表如右表:经测算,平均每辆单车每年可以带来收入500元,不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且以频率作为每辆单车使用寿命的概率,如果你是![]() 公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
参考公式:回归直线方程为![]() ,其中
,其中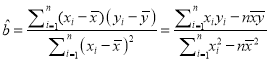 ,
, ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】以下表格记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以![]() 表示.
表示.
甲组 | 9 | 9 | 11 | 11 |
乙组 |
| 8 | 9 | 10 |
(1)如果![]() ,求乙组同学植树棵数的平均数和方差;
,求乙组同学植树棵数的平均数和方差;
(2)如果![]() ,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),将曲线
为参数),将曲线![]() 上各点的横坐标都缩短为原来的
上各点的横坐标都缩短为原来的![]() 倍,纵坐标坐标都伸长为原来的
倍,纵坐标坐标都伸长为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,在极坐标系(与直角坐标系
,在极坐标系(与直角坐标系![]() 取相同的单位长度,且以原点
取相同的单位长度,且以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,M、N分别是AB、BC的中点.

(1)求证:MN∥平面A1B1C1D1
(2)求证:平面B1MN⊥平面BB1D1D.
查看答案和解析>>
科目: 来源: 题型:
【题目】过圆![]() 与
与![]() 轴正半轴的交点A作圆O的切线
轴正半轴的交点A作圆O的切线![]() ,M为
,M为![]() 上任意一点,过M作圆O的另一条切线,切点为Q.当点M在直线
上任意一点,过M作圆O的另一条切线,切点为Q.当点M在直线![]() 上运动时,△MAQ的垂心的轨迹方程为________.
上运动时,△MAQ的垂心的轨迹方程为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,对称轴为坐标轴,椭圆
的中心在原点,对称轴为坐标轴,椭圆![]() 与直线
与直线![]() 相切于点
相切于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() :
: ![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点(
两点(![]() ,
, ![]() 不是长轴端点),且以
不是长轴端点),且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 在
在![]() 轴正半轴上的顶点,求证:直线过定点,并求出该定点的坐标.
轴正半轴上的顶点,求证:直线过定点,并求出该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com