【题目】已知中，三个内角，，所对的边分别是，，．

（1）证明：；

（2）在①，②，③这三个条件中任选一个补充在下面问题中，并解答

若，，________，求的周长．

（1）若G为AD边的中点，求证：BG⊥平面PAD；

（2）求证：AD⊥PB．

【题目】在中，，以的中线为折痕，将沿折起，如图所示，构成二面角,在面内作，且．

（1）求证：∥平面；

（2）如果二面角的大小为，求二面角的余弦值．

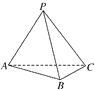
A. AP⊥PB，AP⊥PC

B. AP⊥PB，BC⊥PB

C. 平面BPC⊥平面APC，BC⊥PC

D. AP⊥平面PBC

【题目】共享单车是指企业在校园、地铁站点、公共站点、居民区、商业区、公共服务区等提供自行车单车共享服务，是一种分时租赁模式，是共享经济的一种新形态.某共享单车企业在城市就“一天中一辆单车的平均成本与租用单车数量之间的关系”进行了调查，并将相关数据统计如下表：

根据以上数据，研究人员设计了两种不同的回归分析模型，得到两个拟合函数：

模型甲： ，模型乙： .

（1）为了评价两种模型的拟合效果，完成以下任务：

①完成下表（计算结果精确到0.1元）（备注： ， 称为相应于点的残差）；

②分别计算模型甲与模型乙的残差平方和及，并通过比较， 的大小，判断哪个模型拟合效果更好.

（2）这家企业在城市投放共享单车后，受到广大市民的热烈欢迎并供不应求，于是该企业决定增加单车投放量.根据市场调查，市场投放量达到1万辆时，平均每辆单车一天能收入7.2元；市场投放量达到1.2万辆时，平均每辆单车一天能收入6.8元.若按（1）中拟合效果较好的模型计算一天中一辆单车的平均成本，问该企业投放量选择1万辆还是1.2万辆能获得更多利润？请说明理由.（利润=收入-成本）

【题目】已知抛物线的对称轴为坐标轴，顶点是坐标原点，准线方程为，直线与抛物线相交于不同的， 两点．

（1）求抛物线的标准方程；

（2）如果直线过抛物线的焦点，求的值；

（3）如果，直线是否过一定点，若过一定点，求出该定点；若不过一定点，试说明理由．

【题目】如图，在直三棱柱 中，D为A1B1的中点，AB＝BC＝2，,，则异面直线BD与AC所成的角为（　　）

A. 30°B. 45°C. 60°D. 90°

(1)求中二等奖的概率．

(2)求不中奖的概率．

（Ⅰ）求频率分布直方图中a的值；

（Ⅱ）求这1000名消费者的棕子购买量在600g～1400g的人数；

（Ⅲ）求这1000名消费者的人均粽子购买量（频率分布直方图中同一组的数据用该组区间的中点值作代表）．

【题目】已知函数在上是增函数，则的取值范围是（　　）

A. B. C. D.

【答案】C

【解析】

若函数f（x）=log2（x2﹣ax+3a）在[2，+∞）上是增函数，则x2﹣ax+3a＞0且f（2）＞0，根据二次函数的单调性，我们可得到关于a的不等式，解不等式即可得到a的取值范围．

若函数f（x）=log2（x2﹣ax+3a）在[2，+∞）上是增函数，

则当x∈[2，+∞）时，

x2﹣ax+3a＞0且函数f（x）=x2﹣ax+3a为增函数

即，f（2）=4+a＞0

解得﹣4＜a≤4

故选：C．

【点睛】

本题考查的知识点是复合函数的单调性，二次函数的性质，对数函数的单调区间，其中根据复合函数的单调性，构造关于a的不等式，是解答本题的关键．

【题型】单选题
【结束】
10

【题目】圆锥的高和底面半径之比，且圆锥的体积，则圆锥的表面积为（　　）

A. B. C. D.