
科目: 来源: 题型:
【题目】为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
抽取次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
零件尺寸 | 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
零件尺寸 | 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() ,
, 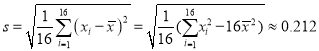 ,
, 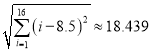 ,
, ![]() ,其中
,其中![]() 为抽取的第
为抽取的第![]() 个零件的尺寸,
个零件的尺寸, ![]() .
.
(1)求![]()
![]() 的相关系数
的相关系数![]() ,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若
,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若![]() ,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).
,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)从这一天抽检的结果看,是否需对当天的生产过程进行检查?
(ⅱ)在![]() 之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的均值与标准差.(精确到0.01)
之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的均值与标准差.(精确到0.01)
附:样本![]()
![]() 的相关系数
的相关系数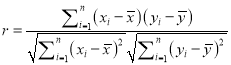 ,
, ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】返乡创业的大学生一直是人们比较关注的对象,他们从大学毕业,没有选择经济发达的大城市,而是回到自己的家乡,为养育自己的家乡贡献自己的力量,在享有“国际花园城市”称号的温江幸福田园,就有一个由大学毕业生创办的农家院“小时代”,其独特的装修风格和经营模式,引来无数人的关注,带来红红火火的现状,给青年大学生们就业创业上很多新的启示.在接受采访中,该老板谈起以下情况:初期投入为72万元,经营后每年的总收入为50万元,第n年需要付出房屋维护和工人工资等费用是首项为12,公差为4的等差数列![]() (单位:万元).
(单位:万元).
(1)求![]() ;
;
(2)该农家乐第几年开始盈利?能盈利几年?(即总收入减去成本及所有费用之差为正值)
(3)该农家乐经营多少年,其年平均获利最大?年平均获利的最大值是多少?(年平均获利![]() 前
前![]() 年总获利
年总获利![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】某射击手在同一条件下进行射击训练,结果如下:
射击次数n | 10 | 20 | 50 | 100 | 200 | 500 |
击中靶心次数m | 8 | 19 | 44 | 92 | 178 | 455 |
击中靶心频率 |
(1)求出表中击中靶心的各个频率值;
(2)这个射击手射击一次,击中靶心的概率可估计为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】设椭圆![]() 的离心率
的离心率![]() ,左焦点为
,左焦点为![]() ,右顶点为
,右顶点为![]() ,过点
,过点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,若直线
两点,若直线![]() 垂直于
垂直于![]() 轴时,有
轴时,有![]() .
.
(1)求椭圆的方程;
(2)设直线![]() :
: ![]() 上两点
上两点![]() ,
, ![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与椭圆相交于点
与椭圆相交于点![]() (
(![]() 异于点
异于点![]() ),直线
),直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .若
.若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】气象意义上从春季进入夏季的标志为:“连续5天的日平均温度均不低于![]() ”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):
”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体均值为24;
③丙地:5个数据中有一个数据是32,总体均值为26,总体方差为10.8;
则肯定进入夏季的地区有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台机床生产的零件各100件进行检测,检测结果统计如下:
测试指标 | [85,90) | [90,95) | [95,100) | [100,105) | [105,110) |
甲机床 | 8 | 12 | 40 | 32 | 8 |
乙机床 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计甲机床、乙机床生产的零件为优品的概率;
(2)甲机床生产1件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20元,假设甲机床某天生产50件零件,请估计甲机床该天的利润(单位:元);
(3)从甲、乙机床生产的零件指标在[90,95)内的零件中,采用分层抽样的方法抽取5件,从这5件中任意抽取2件进行质量分析,求这2件都是乙机床生产的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】有以下四种变换方式:
![]() 向左平移
向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍
倍![]() 纵坐标不变
纵坐标不变![]() ;
;
![]() 向左平移
向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍
倍![]() 纵坐标不变
纵坐标不变![]() ;
;
![]() 把各点的横坐标缩短到原来的
把各点的横坐标缩短到原来的![]() 倍
倍![]() 纵坐标不变
纵坐标不变![]() ,再向左平移
,再向左平移![]() 个单位长度;
个单位长度;
![]() 把各点的横坐标缩短到原来的
把各点的横坐标缩短到原来的![]() 倍
倍![]() 纵坐标不变
纵坐标不变![]() ,再向左平移
,再向左平移![]() 个单位长度;
个单位长度;
其中能将函数![]() 的图象变为函数
的图象变为函数![]() 的图象的是
的图象的是![]()
![]()
A. ![]() 和
和![]() B.
B. ![]() 和
和![]() C.
C. ![]() 和
和![]() D.
D. ![]() 和
和![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市随机选取![]() 位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
| 甲 | 乙 | 丙 | 丁 |
| √ | × | √ | √ |
| × | √ | × | √ |
| √ | √ | √ | × |
| √ | × | √ | × |
85 | √ | × | × | × |
| × | √ | × | × |
(Ⅰ)估计顾客同时购买乙和丙的概率;
(Ⅱ)估计顾客在甲、乙、丙、丁中同时购买![]() 中商品的概率;
中商品的概率;
(Ⅲ)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】新鲜的荔枝很好吃,但摘下后容易变黑,影响卖相.某大型超市进行扶贫工作,按计划每年六月从精准扶贫户中订购荔枝,每天进货量相同且每公斤20元,售价为每公斤24元,未售完的荔枝降价处理,以每公斤16元的价格当天全部处理完.根据往年情况,每天需求量与当天平均气温有关.如果平均气温不低于25摄氏度,需求量为![]() 公斤;如果平均气温位于
公斤;如果平均气温位于![]() 摄氏度,需求量为
摄氏度,需求量为![]() 公斤;如果平均气温位于
公斤;如果平均气温位于![]() 摄氏度,需求量为
摄氏度,需求量为![]() 公斤;如果平均气温低于15摄氏度,需求量为
公斤;如果平均气温低于15摄氏度,需求量为![]() 公斤.为了确定6月1日到30日的订购数量,统计了前三年6月1日到30日各天的平均气温数据,得到如图所示的频数分布表:
公斤.为了确定6月1日到30日的订购数量,统计了前三年6月1日到30日各天的平均气温数据,得到如图所示的频数分布表:
平均气温 |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
(Ⅰ)假设该商场在这90天内每天进货100公斤,求这90天荔枝每天为该商场带来的平均利润(结果取整数);
(Ⅱ)若该商场每天进货量为200公斤,以这90天记录的各需求量的频率作为各需求量发生的概率,求当天该商场不亏损的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com