
科目: 来源: 题型:
【题目】![]() ,
,![]() 两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
![]() 组:10,11,12,13,14,15,16
组:10,11,12,13,14,15,16
![]() 组:12,13,15,16,17,14,
组:12,13,15,16,17,14,![]()
假设所有病人的康复时间互相独立,从![]() ,
,![]() 两组随机各选1人,
两组随机各选1人,![]() 组选出的人记为甲,
组选出的人记为甲,![]() 组选出的
组选出的
人记为乙.
(Ⅰ)求甲的康复时间不少于14天的概率;
(Ⅱ)如果![]() ,求甲的康复时间比乙的康复时间长的概率;
,求甲的康复时间比乙的康复时间长的概率;
(Ⅲ)当![]() 为何值时,
为何值时,![]() ,
,![]() 两组病人康复时间的方差相等?(结论不要求证明)
两组病人康复时间的方差相等?(结论不要求证明)
查看答案和解析>>
科目: 来源: 题型:
【题目】近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的分类垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1 000吨生活垃圾,数据统计如下(单位:吨):
“厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
厨余垃圾 | 400 | 100 | 100 |
可回收物 | 30 | 240 | 30 |
其他垃圾 | 20 | 20 | 60 |
(1)试估计厨余垃圾投放正确的概率P;
(2)试估计生活垃圾投放错误的概率;
(3)假设厨余垃圾在“厨余垃圾”箱,“可回收物”箱,“其他垃圾”箱的投放量分别为a、b、c,其中a>0,a+b+c=600. 当数据a、b、c的方差s2最大时,写出a、b、c的值(结论不要求证明),并求出此时s2的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】一种电路控制器在出厂时,每3件一等品应装成一箱,工人装箱时,不小心将2件二等品和1件一等品装入了一箱,为了找出该箱中的二等品,对该箱中的产品逐件进行测试,假设检测员不知道该箱产品中二等品的具体数量,求:
(1)仅测试2件就找到全部二等品的概率;
(2)测试的第2件产品是二等品的概率;
(3)到第3次才测试出全部二等品的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业2017年的纯利润为500万元,因设备老化等原因,企业的生产能力逐年下降,若不能进行技术改造,预测从2018年起每年比上一年纯利润减少20万元,2018年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第![]() 年(以2018年为第一年)的利润为
年(以2018年为第一年)的利润为![]() 万元(
万元(![]() 为正整数).
为正整数).
(1)设从今年起的前![]() 年,若该企业不进行技术改造的累计纯利润为
年,若该企业不进行技术改造的累计纯利润为![]() 万元,进行技术改造后的累计纯利润为
万元,进行技术改造后的累计纯利润为![]() 万元(须扣除技术改造资金),求
万元(须扣除技术改造资金),求![]() ,
,![]() 的表达式;
的表达式;
(2)依上述预测,从2018年起该企业至少经过多少年,进行技术改造后的累计利润超过不进行技术改造的累计纯利润?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,坐标原点为
,坐标原点为![]() .椭圆
.椭圆![]() 的动弦
的动弦![]() 过右焦点
过右焦点![]() 且不垂直于坐标轴,
且不垂直于坐标轴, ![]() 的中点为
的中点为![]() ,过
,过![]() 且垂直于线段
且垂直于线段![]() 的直线交射线
的直线交射线![]() 于点
于点![]()
(I)证明:点![]() 在直线
在直线![]() 上;
上;
(Ⅱ)当四边形![]() 是平行四边形时,求
是平行四边形时,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从种植有甲、乙两种麦苗的两块试验田中各抽取6株麦苗测量株高,得到的数据如下(单位:cm):
甲:9,10,11,12,10,20;
С:8,14,13,10,12,21.
(1)选择合适的统计图表表示上述数据;
(2)分别计算两组数据的平均数与方差,并由此判断甲、乙两种麦苗的长势情况.
查看答案和解析>>
科目: 来源: 题型:
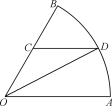
【题目】如图是一个半径为2千米,圆心角为![]() 的扇形游览区的平面示意图
的扇形游览区的平面示意图![]() 是半径
是半径![]() 上一点,
上一点,![]() 是圆弧
是圆弧![]() 上一点,且
上一点,且![]() .现在线段
.现在线段![]() ,线段
,线段![]() 及圆弧
及圆弧![]() 三段所示位置设立广告位,经测算广告位出租收入是:线段
三段所示位置设立广告位,经测算广告位出租收入是:线段![]() 处每千米为
处每千米为![]() 元,线段
元,线段![]() 及圆弧
及圆弧![]() 处每千米均为
处每千米均为![]() 元.设
元.设![]() 弧度,广告位出租的总收入为
弧度,广告位出租的总收入为![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)试问:![]() 为何值时,广告位出租的总收入最大?并求出其最大值.
为何值时,广告位出租的总收入最大?并求出其最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com