
科目: 来源: 题型:
【题目】一只红铃虫的产卵数![]() 和温度
和温度![]() 有关,现收集了6组观测数据如下表:
有关,现收集了6组观测数据如下表:
温度 | 21 | 24 | 25 | 27 | 29 | 32 |
产卵数 | 7 | 11 | 21 | 24 | 66 | 115 |
| 1.946 | 2.398 | 3.045 | 3.178 | 4.191 | 4.745 |
(I)以温度为23、25、27、29的数据分别建立:①![]() 和
和![]() 之间线性回归方程
之间线性回归方程![]() ,②
,②![]() 和
和![]() 之间线性回归方程
之间线性回归方程![]() ;
;
(Ⅱ)若以(Ⅰ)所得回归方程预测,得到温度为21、32的数据如下:
温度 | 21 | 32 |
| -11.5 | 80.94 |
| 1.825 | 4.857 |
试以上表数据说明①②两个模型,哪个拟合的效果更好.
参考数据:![]()
![]()
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 离心率为
离心率为![]() ,四个顶点构成的四边形的面积是4.
,四个顶点构成的四边形的面积是4.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 均在第一象限,
均在第一象限,![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,设直线
两点,设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,且
,且![]() (其中
(其中![]() 为坐标原点).证明: 直线
为坐标原点).证明: 直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】因客流量临时增大,某鞋店拟用一个高为50![]() (即
(即![]() )的平面镜自制一个竖直摆放的简易鞋镜,根据经验:一般顾客
)的平面镜自制一个竖直摆放的简易鞋镜,根据经验:一般顾客![]() 的眼睛
的眼睛![]() 到地面的距离为
到地面的距离为![]() (
(![]() )在区间
)在区间![]() 内,设支架
内,设支架![]() 高为
高为![]() (
(![]() )
)![]() ,
,![]() ,顾客可视的镜像范围为
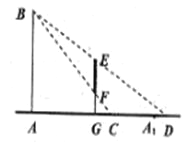
,顾客可视的镜像范围为![]() (如图所示),记
(如图所示),记![]() 的长度为
的长度为![]() (
(![]() ).
).
(I)当![]() 时,试求
时,试求![]() 关于
关于![]() 的函数关系式和
的函数关系式和![]() 的最大值;
的最大值;
(II)当顾客的鞋![]() 在镜中的像
在镜中的像![]() 满足不等关系
满足不等关系![]() (不计鞋长)时,称顾客可在镜中看到自己的鞋,若使一般顾客都能在镜中看到自己的鞋,试求
(不计鞋长)时,称顾客可在镜中看到自己的鞋,若使一般顾客都能在镜中看到自己的鞋,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】(2016高考新课标II,理15)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解高校学生平均每天使用手机的时间长短是否与性别有关,某调查小组随机抽取了25 名男生、10名女生进行为期一周的跟踪调查,调查结果如表所示:
平均每天使用手机 | 平均每天使用手机 | 合计 | |
男生 | 15 | 10 | 25 |
女生 | 3 | 7 | 10 |
合计 | 18 | 17 | 35 |
(I) 根据列联表判断,是否有90%的把握认为学生使用手机的时间长短与性别有关;
(II)在参与调查的平均每天使用手机不超过3小时的10名男生中,有6人使用国产手机,从这10名男生中任意选取3人,求这3人中使用国产手机的人数![]() 的分布列和数学期望.
的分布列和数学期望.
| 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
参考公式:![]()
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】现有4种不同颜色要对如图所示的四个部分进行着色,要求有公共边界的两部分不能用同一种颜色,则不同的着色方法共有( )

A. 144种 B. 72种 C. 64种 D. 84种
查看答案和解析>>
科目: 来源: 题型:
【题目】某种产品的广告费用支出x(万元)与销售额y(万元)之间有如下的对应数据:

(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为9万元时,销售收入y的值.
注:①参考公式:线性回归方程系数公式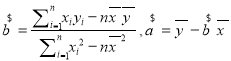 ;
;
②参考数据:![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为调查高三年级学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图1)和女生身高情况的频率分布直方图(图2).已知图1中身高在170~175cm的男生人数有16人
.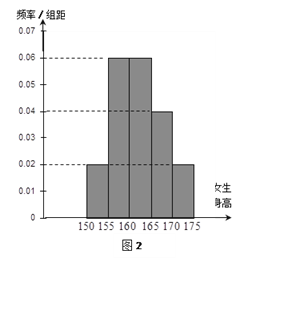

(1)根据频率分布直方图,完成下列的![]() 列联表,并判断能有多大(百分比)的把握认为“身高与性别有关”?
列联表,并判断能有多大(百分比)的把握认为“身高与性别有关”?
|
| 总计 | |
男生身高 | |||
女生身高 | |||
总计 |
(2)在上述80名学生中,从身高在170-175cm之间的学生按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
| 0.025 | 0.610 | 0.005 | 0.001 |
| 5.024 | 4.635 | 7.879 | 10.828 |
参考公式及参考数据如下:
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂现有职工320人,平均每人每年可创利20万元.该工厂打算购进一批智能机器人(每购进一台机器人,将有一名职工下岗).据测算,如果购进智能机器人不超过100台,每购进一台机器人,所有留岗职工(机器人视为机器,不作为职工看待)在机器人的帮助下,每人每年多创利2千元,每台机器人购置费及日常维护费用折合后平均每年2万元,工厂为体现对职工的关心,给予下岗职工每人每年4万元补贴;如果购进智能机器人数量超过100台,则工厂的年利润![]() 万元(x为机器人台数且x<320).
万元(x为机器人台数且x<320).
(1)写出工厂的年利润y与购进智能机器人台数x的函数关系.
(2)为获得最大经济效益,工厂应购进多少台智能机器人?此时工厂的最大年利润是多少?(参考数据:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com