
科目: 来源: 题型:
【题目】对于函数 ,下列
,下列![]() 个结论正确的是__________(把你认为正确的答案全部写上).
个结论正确的是__________(把你认为正确的答案全部写上).
(1)任取![]() ,都有
,都有![]() ;
;
(2)函数![]() 在
在![]() 上单调递增;
上单调递增;
(3)![]() ,对一切
,对一切![]() 恒成立;
恒成立;
(4)函数![]() 有
有![]() 个零点;
个零点;
(5)若关于![]() 的方程
的方程![]() 有且只有两个不同的实根
有且只有两个不同的实根![]() ,
,![]() ,则
,则![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知下列命题:
①在某项测量中,测量结果![]() 服从正态分布
服从正态分布![]() ,若
,若![]() 在
在![]() 内取值范围概率为
内取值范围概率为![]() ,则
,则![]() 在
在![]() 内取值的概率为
内取值的概率为![]() ;
;
②若![]() ,
,![]() 为实数,则“
为实数,则“![]() ”是“
”是“![]() ”的充分而不必要条件;
”的充分而不必要条件;
③已知命题![]() ,
,![]() ,则
,则![]() 是:
是:
![]() ,
,![]() ;
;
④![]() 中,“角
中,“角![]() ,
,![]() ,
,![]() 成等差数列”是“
成等差数列”是“![]() ”的充分不必要条件;其中,所有真命题的个数是( )
”的充分不必要条件;其中,所有真命题的个数是( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,菱形ABCD与正三角形BCE的边长均为2,且平面ABCD⊥平面BCE,![]() 平面ABCD,
平面ABCD,![]() .
.

(I)求证:![]() 平面ABCD;
平面ABCD;
(II)求证:平面ACF⊥平面BDF.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面几种推理是合情推理的是( )
①由圆的性质类比出球的有关性质;②由直角三角形、等腰三角形、等边三角形内角和是![]() 归纳出所有三角形的内角和都是
归纳出所有三角形的内角和都是![]() ;③由
;③由![]() ,满足
,满足![]() ,
,![]() ,推出
,推出![]() 是奇函数;④三角形内角和是
是奇函数;④三角形内角和是![]() ,四边形内角和是
,四边形内角和是![]() ,五边形内角和是
,五边形内角和是![]() ,由此得凸多边形内角和是
,由此得凸多边形内角和是![]() .
.
A. ①②B. ①③④C. ①②④D. ②④
查看答案和解析>>
科目: 来源: 题型:
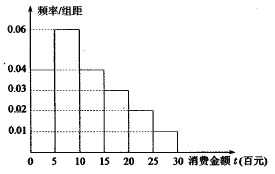
【题目】“双十一”已经成为网民们的网购狂欢节,某电子商务平台对某市的网民在今年“双十一”的网购情况进行摸底调查,用随机抽样的方法抽取了100人,其消费金额![]() (百元)的频率分布直方图如图所示:
(百元)的频率分布直方图如图所示:
(1)求网民消费金额![]() 的平均值和中位数
的平均值和中位数![]() ;
;
(2)把下表中空格里的数填上,能否有![]() 的把握认为网购消费与性别有关;
的把握认为网购消费与性别有关;
男 | 女 | 合计 | |
| |||
| 30 | ||
合计 | 45 |
附表:
|
|
|
|
|
|
|
|
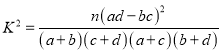 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】从![]() 年
年![]() 月份,某市街头出现共享单车,到
月份,某市街头出现共享单车,到![]() 月份,根据统计,市区所有人骑行过共享单车的人数已占
月份,根据统计,市区所有人骑行过共享单车的人数已占![]() ,骑行过共享单车的人数中,有
,骑行过共享单车的人数中,有![]() 是大学生(含大中专及高职),该市区人口按
是大学生(含大中专及高职),该市区人口按![]() 万计算,大学生人数约
万计算,大学生人数约![]() 万人.
万人.
(1)任选出一名大学生,求他(她)骑行过共享单车的概率;
(2)随单车投放数量增加,乱停乱放成为城市管理的问题,以下是累计投放单车数量![]() 与乱停乱放单车数量
与乱停乱放单车数量![]() 之间的关系图表:
之间的关系图表:
累计投放单车数量 |
|
|
|
|
|
乱停乱放单车数量 |
|
|
|
|
|
①计算![]() 关于
关于![]() 的线性回归方程(其中
的线性回归方程(其中![]() 精确到
精确到![]() 值保留三位有效数字),并预测当
值保留三位有效数字),并预测当![]() 时,单车乱停乱放的数量;
时,单车乱停乱放的数量;
②已知该市共有五个区,其中有两个区的单车乱停乱放数量超过标准.在“双创”活动中,检查组随机抽取三个区调查单车乱停乱放数量, ![]() 表示“单车乱停乱放数量超过标准的区的个数”,求
表示“单车乱停乱放数量超过标准的区的个数”,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
参考公式和数据:回归直线方程![]() 中的斜率和截距的最小二乘法估计公式分别为
中的斜率和截距的最小二乘法估计公式分别为
![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人投篮命中的概率分别为![]() 与
与![]() ,各自相互独立.现两人做投篮游戏,共比赛3局,每局每人各投一球.
,各自相互独立.现两人做投篮游戏,共比赛3局,每局每人各投一球.
(1)求比赛结束后甲的进球数比乙的进球数多1的概率;
(2)设![]() 表示比赛结束后甲、乙两人进球数的差的绝对值,求
表示比赛结束后甲、乙两人进球数的差的绝对值,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
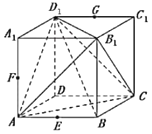
【题目】已知正方体ABCD-A1B1C1D1的棱长为a,点E,F,G分别为棱AB,AA1,C1D1的中点.下列结论中,正确结论的序号是______.
①过E,F,G三点作正方体的截面,所得截面为正六边形;
②B1D1∥平面EFG;
③BD1⊥平面ACB1;
④异面直线EF与BD1所成角的正切值为![]() ;
;
⑤四面体ACB1D1的体积等于![]() a3
a3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com