
科目: 来源: 题型:
【题目】两次购买同一种物品,可以用两种不同的策略,第一种是不考虑物品价格的升降,每次购买这种物品的数量一定;第二种是不考虑物品价格的升降,每次购买这种物品所花的钱数一定.哪种购物方式比较经济?你能把所得结论作一些推广吗?
查看答案和解析>>
科目: 来源: 题型:
【题目】在中国决胜全面建成小康社会的关键之年,如何更好地保障和改善民生,如何切实增强政策“获得感”,成为![]() 年全国两会的重要关切.某地区为改善民生调研了甲、乙、丙、丁、戊
年全国两会的重要关切.某地区为改善民生调研了甲、乙、丙、丁、戊![]() 个民生项目,得到如下信息:①若该地区引进甲项目,就必须引进与之配套的乙项目;②丁、戊两个项目与民生密切相关,这两个项目至少要引进一个;③乙、丙两个项目之间有冲突,两个项目只能引进一个;④丙、丁两个项目关联度较高,要么同时引进,要么都不引进;⑤若引进项目戊,甲、丁两个项目也必须引进.则该地区应引进的项目为( )
个民生项目,得到如下信息:①若该地区引进甲项目,就必须引进与之配套的乙项目;②丁、戊两个项目与民生密切相关,这两个项目至少要引进一个;③乙、丙两个项目之间有冲突,两个项目只能引进一个;④丙、丁两个项目关联度较高,要么同时引进,要么都不引进;⑤若引进项目戊,甲、丁两个项目也必须引进.则该地区应引进的项目为( )
A. 甲、乙B. 丙、丁C. 乙、丁D. 甲、丙
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和直线
的普通方程和直线![]() 的倾斜角;
的倾斜角;
(2)设点![]() 和
和![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆心为![]() 的圆过原点
的圆过原点![]() ,且直线
,且直线![]() 与圆
与圆![]() 相切于点
相切于点![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)已知过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,且直线
,且直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点.
两点.
①若![]() ,求弦
,求弦![]() 的长;
的长;
②若圆![]() 上存在点
上存在点![]() ,使得
,使得![]() 成立,求直线
成立,求直线![]() 的斜率
的斜率![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分12分)已知椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,离心率为
,离心率为![]() ,其右焦点为
,其右焦点为![]() ,过点
,过点![]() 作直线交椭圆于另一点
作直线交椭圆于另一点![]() .
.
(1)若![]() ,求
,求![]() 外接圆的方程;
外接圆的方程;
(2)若过点![]() 的直线与椭圆
的直线与椭圆![]()
![]() 相交于两点
相交于两点![]() 、
、![]() ,设
,设![]() 为
为![]() 上一点,且满足
上一点,且满足![]() (
(![]() 为坐标原点),当
为坐标原点),当![]() 时,求实数
时,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.

(1)证明: ![]() ;
;
(2)设![]() 为线段
为线段![]() 上的动点,若线段
上的动点,若线段![]() 长的最小值为
长的最小值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)证明线线垂直则需证明线面垂直,根据题意易得![]() ,然后根据等边三角形的性质可得
,然后根据等边三角形的性质可得![]() ,又
,又![]() ,因此
,因此![]() 得
得![]() 平面
平面![]() ,从而得证(2)先找到EH什么时候最短,显然当线段
,从而得证(2)先找到EH什么时候最短,显然当线段![]() 长的最小时,
长的最小时, ![]() ,在
,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,由
,由![]() 中,
中, ![]() ,
, ![]() ,∴
,∴![]() .然后建立空间直角坐标系,写出两个面法向量再根据向量的夹角公式即可得余弦值
.然后建立空间直角坐标系,写出两个面法向量再根据向量的夹角公式即可得余弦值
解析:(1)证明:∵四边形![]() 为菱形,
为菱形, ![]() ,
,
∴![]() 为正三角形.又
为正三角形.又![]() 为
为![]() 的中点,∴
的中点,∴![]() .
.
又![]() ,因此
,因此![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() .
.
而![]() 平面
平面![]() ,
, ![]() 平面
平面![]() 且
且![]() ,
,
∴![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,∴
,∴![]() .
.

(2)如图, ![]() 为
为![]() 上任意一点,连接
上任意一点,连接![]() ,
, ![]() .
.

当线段![]() 长的最小时,
长的最小时, ![]() ,由(1)知
,由(1)知![]() ,
,
∴![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,故
,故![]() .
.
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
由![]() 中,
中, ![]() ,
, ![]() ,∴
,∴![]() .
.
由(1)知![]() ,
, ![]() ,
, ![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,建立如图所示的空间直角坐标系,又
为坐标原点,建立如图所示的空间直角坐标系,又![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,
的中点,
可得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, 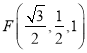 ,
,
所以![]() ,
,  .
.
设平面![]() 的一法向量为
的一法向量为![]() ,
,
则![]() 因此
因此 ,
,
取![]() ,则
,则![]() ,
,
因为![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,
,
故![]() 为平面
为平面![]() 的一法向量.又
的一法向量.又![]() ,
,
所以![]()

![]() .
.
易得二面角![]() 为锐角,故所求二面角的余弦值为
为锐角,故所求二面角的余弦值为![]() .
.

【题型】解答题
【结束】
20
【题目】【2018湖北七市(州)教研协作体3月高三联考】已知椭圆![]() :
: ![]()
![]() 的左顶点为
的左顶点为![]() ,上顶点为
,上顶点为![]() ,直线
,直线![]() 与直线
与直线![]() 垂直,垂足为
垂直,垂足为![]() 点,且点
点,且点![]() 是线段
是线段![]() 的中点.
的中点.

(I)求椭圆![]() 的方程;
的方程;
(II)如图,若直线![]() :
: ![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,点
两点,点![]() 在椭圆
在椭圆![]() 上,且四边形
上,且四边形![]() 为平行四边形,求证:四边形
为平行四边形,求证:四边形![]() 的面积
的面积![]() 为定值.
为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校倡导为特困学生募捐,要求在自动购水机处每购买一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出矿泉水箱数和收入情况,列表如下:
售出水量 | 7 | 6 | 6 | 5 | 6 |
收入 | 165 | 142 | 148 | 125 | 150 |
学校计划将捐款以奖学金的形式奖励给品学兼优的特困生,规定:特困生综合考核前20名,获一等奖学金500元;综合考核21-50名,获二等奖学金300元;综合考核50名以后的不获得奖学金.
(1)若![]() 与
与![]() 成线性相关,则某天售出9箱水时,预计收入为多少元?
成线性相关,则某天售出9箱水时,预计收入为多少元?
(2)甲乙两名学生获一等奖学金的概率均为![]() ,获二等奖学金的概率均为
,获二等奖学金的概率均为![]() ,不获得奖学金的概率均为
,不获得奖学金的概率均为![]() ,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和
,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和![]() 的分布列及数学期望;
的分布列及数学期望;
附:回归方程![]() ,其中
,其中 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com