
科目: 来源: 题型:
【题目】设函数![]() 为定义在
为定义在![]() 上的奇函数,且当
上的奇函数,且当![]() 时,
时,![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求实数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ;
;
(3)若函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,则记所有满足条件的区间
,则记所有满足条件的区间![]() 的并集为
的并集为![]() ,设
,设![]() ,问是否存在实数
,问是否存在实数![]() ,使得集合
,使得集合![]()
![]() 恰含有
恰含有![]() 个元素?若存在,求出
个元素?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M,N分别是AD,BE的中点,将三角形ADE沿AE折起,则下列说法正确的是________(填序号).
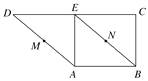
①不论D折至何位置(不在平面ABC内),都有MN∥平面DEC;②不论D折至何位置,都有MN⊥AE;③不论D折至何位置(不在平面ABC内),都有MN∥AB;④在折起过程中,一定存在某个位置,使EC⊥AD.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,
,![]() 是
是![]() 上任意一点。
上任意一点。

(1)求证:![]() ;
;
(2)当![]() 面积的最小值是9时,在线段
面积的最小值是9时,在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 与平面
与平面![]() 所成角的正切值为2?若存在?求出
所成角的正切值为2?若存在?求出![]() 的值,若不存在,请说明理由
的值,若不存在,请说明理由
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,圆
轴正半轴为极轴的极坐标系中,圆![]() 的方程为
的方程为![]() .
.
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年高考前夕某地天空出现了一朵点赞云,为了将这朵祥云送给马上升高三的各位学子,现以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,在直角坐标系
,在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).

(1)求曲线![]() 的直角坐标方程:
的直角坐标方程:
(2)点![]() 为曲线
为曲线![]() 上任意一点,点
上任意一点,点![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的最小值。
的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com